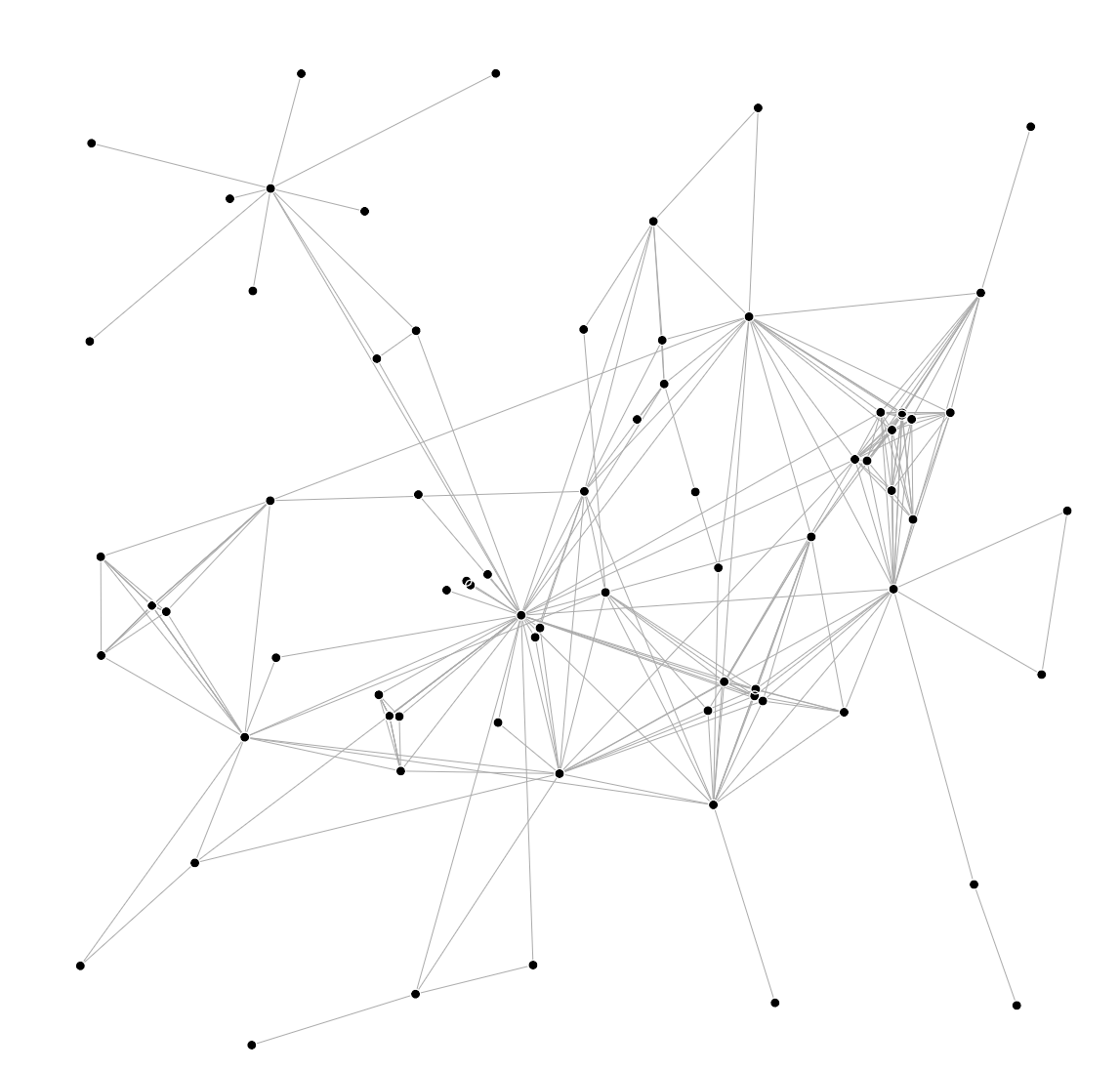
After Self-Organizing Graphs: A Neural Network Perspective of Graph Layout by Bernd Meyer.
npm install `isom-layout`;
import som from 'isom-layout';
const graph = {
nodes: [
{ id: 0, data: ...},
{ id: 1, data: ...},
...
],
edges: [
{ source: 0, target: 1, data: ...},
...
]
};
// if your nodes have no initial positions
som.randomize(graph, bounds);
// modifies coord in-place
som(graph, {
// other options, see below
bounds: bounds, // [xmin, ymin, xmax, ymax],
onUpdate: () => {
// do your rendering here
},
onEnd: () => {
// converged
}
});To understand the options you need to know a bit about how algorithm works. Basically, it
- picks random points in the graph space
- finds the closest node to this random location
- using kind of BFS it continiously pulls the nodes and its neighbours in the direction of the random point.
- while sweeps are repeated, cooling effect takes place, reducing the pulling force
- also the radius gets gradually reduced so that during the last stage smaller areas of graph are getting changed
som(graph, options)
maxIterationsMaximum algorithm sweeps. default2000adaptionInitial force value. default0.8radiusMaximum graph-theoretical distance of the nodes involved in one sweep. default3coolingFactorCooling speed, see the cooling equation, default2iterationsPerRadiusStepHow fast the radius is decreased. default70iterationsPerUpdateHow many iterations to perform between the "ticks", default10- for demo purposes. For the default params it means that the algorithm will re-render every 10ms, 200 renders in totalupdateDelayDelay between the update groups. default0onUpdateUpdate callback. Put your rendering hereonEndComplete callbackboundsCoordinate space boundaries.[xmin,ymin,xmax,ymax]. If not provided, algorithm will attempt to calculate them from the current nodes positions. So eitherboundsor initial coordinates have to be provideddontRandomizeDon't re-shuffle the node positions. defaultfalse
My impression - useless. The only thing it shows more or less is the nodes with highest degrees. Maybe it can be good on simple chains. You can endlessly tweak the parametres, but it doesn't give you a nice comprehensible layout. So this a mere exercise in understanding the parameters and nature of the algorithms like this one.
Also funny observation: it works as if an impatient person was untangling a threadball by randomly pulling the outstanding knots and strings.
MIT