ProbeInit

The method ProbeInit expects a list of d matrices as argument. These matrices constitute the quantized embedding functions 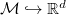. In this sense they define the fuzzy brane embedded in .

• This method takes care of building the appropriate (Laplace-/Dirac-) operator for you which is needed to perform the rasterizing procedure.

• If no starting point for the rasterizing procedure is given via options, the method tries to find one for you.

• The gradient and eigenvalues of the Hesse matrix at the starting point are calculated and printed for inspection.

• ProbeInit tries to guess the correct dimension of the manifold which constitutes the semi-classical limit and prints it for inspection. This guess can be overridden by the ProbeScan option Dimension.

• A guess for an appropriate step size is calculated to get a rough idea of the manifold. The user can (and should) override this guess by the ProbeScan option StepSize.

Note that calling the method ProbeInit is absolutely required before methods of this package with the prefix Probe can be used!

Arguments

ProbeInit has the following (non-optional) arguments:

Argument	Description
list_of_matrices	These matrices constitute the quantized embedding functions 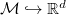. They have to be provided in the form of a Mathematica-List.

Options

ProbeInit admits the following options:

Options	Description
Probe	Possible option values are "Laplace" or "Dirac" respectively its squared version "DiracSq". Default: Probe->"Laplace" Example: Probe->"DiracSq"
Subspace	If one is only interested in a certain subspace of the target space , it is possible to specify a List of numbers which selects the subspace . The one-dimensional subspace corresponds to the i-th quantized embedding function in the List which was provided as argument. Of course, the dimension m of the subspace has to be smaller than the dimension d of the target space 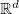. If this option is omitted, no subspace selection takes place. Example: Subspace->{1,3,5}
StartingPoint	In most non-trivial circumstances it makes sense to use different starting points than the automatically determined one, since it might not even be computationally viable to determine a global minimum. In this case the user can specify a point in via a List of m values. If such a point is specified, the program will skip the search for a global minimum, speeding up the procedure immensely. Example: StartingPoint->{0.1,0.2,5.}

Example

(* load the package *)
<< BProbeM`

(* generate a list t consisting of the 3 Pauli matrices *)
t = PauliMatrix[{1,2,3}];

(* initialize the package *)
ProbeInit[t, Probe->"Dirac", Subspace->{1,2}];

This example loads the package, generates a list of three Pauli matrices and uses them to initialize the package. In this case the target space is R^3 where a two-dimensional subspace R^2 is selected.