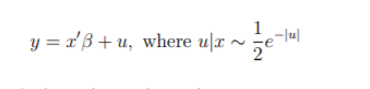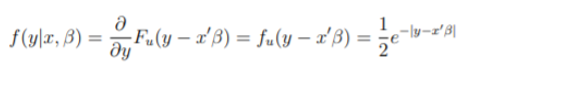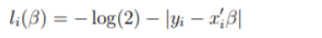numerical-optimization-of-likelihood-function-to-find-MLE-of-LAD-estimator

For econometrics, Maximum Likelihood Estimation is a very popular estimating technique, in which not all estimators have closed form solutions (meaning you can't solve it on paper, you need to compute it!). Maximum likelihood estimates is the estimate which is the maximum of the likelihood of receiving a specific parameter estimate given the data. Meaning the data is most probable in the statistical model given a specific point in the parameter space of the model. The data is also assumed to follow a certain statistical model either a data distribution such as a gaussian distribution, or a linear model such as OLS regression.

The example I am doing is the MLE of the Least-Absolute Deviation estimator. Which compared to OLS, LAD equally weights all samples and therefore is robust to outliers. MLE of the LAD estimator can be represented by this parametic model:

This log of the likeihood function is derived from taking the log of the likelihood pdf of y. The pdf of this model is simply the derivative of the cdf, which is:

I will be maximizing the LAD log likelihood function to find the maximum likelihood estimate.

Creating the model

Since the log likelihood function is an absolute value function, it’s derivative cannot be taken hence no closed form solution. We’re trying to find the max likelihood of theta given x,y. I have created random samples of X and Y using the random and distributions packages to test our model.

using Random, Distributions

x= rand(Normal(),100)
y= rand(Normal(),100)

The only parameter that must be maximized is beta. I created two functions, first the regular log likelihood function and the second the first order conditions for the log likelihood function. Again, since the likelihood function has abs value the derivative cannot be taken, but an approximation can be created using Newton’s difference quotient.

function loglike(Beta)
    llbeta  = -length(x)*log(2)-sum(abs.(y .-x*Beta))
    return -llbeta
end

#newton's difference quotient
function derivat(Beta)
    h = .00001
    g2 = (loglike(Beta + h) - loglike(Beta) ) / h
    return g2
end

Optimization Algorithm - Bisection

Here is the bisection algorithm, which is a rooting finding algorithms that works with continuous functions. The algorithm specifically takes advantage of the fact that when two outputs have different signs, the zero lies somewhere inbetween.

function bisection(fun,a,b,tol)
    sa = sign(fun(a))
    sb = sign(fun(b))
    if sa == sb
        error("Interval is not valid")
    end

    while abs(b-a)>tol
        c = (a+b)/2
        sc = sign(fun(c))
        if sc == 0
            a,b = c,c
        elseif sa==sc
            a,b = c,b
        else
            a,b = a,c
        end
    end
    return (a+b)/2
end

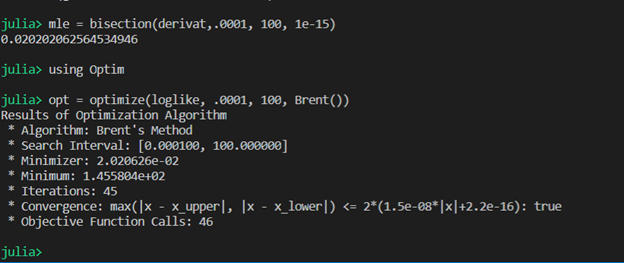
I call my bisection algorithm to optimize the derivative function. I also use the optimize package to also optimize the log like function, just to compare my answers and make sure my bisection algorithm works.

 mle = bisection(derivat,.0001, 100, 1e-15)
using Optim
opt = optimize(loglike, .0001, 100, Brent())

In which a maximum for theta is .0202 for both techniques. This suggest that the coefficient of the lad estimator is .02022.