[toc]
如果可以的话,就坚持下去吧
以下内容仅为自己的一些随笔感想,并非题解
这题没有什么要说的,其实就是用空间换时间
关于这题,我最开始想的是一种很笨的方法,就是我把链表先倒过来转成数组,然后再把两个数组相加,然后再把这个数组转成链表,后来呢尝试了一下,发现太复杂了, 不过这个思路应该还是对的,不过确实太麻烦了。
后来沉下心想了一下,发现其实每次都是只要考虑当前位置的就行了,后面的对与当前的节点只是Next,自然也就可以用递归了。
这是自己第一次用递归解出来链表类的问题,所以还是挺开心的。继续坚持
关于这题,其实最开始看到就是有思路的,但是后面真写的时候发现还是有些地方没有考虑到的
- 关于
right应该在满足什么条件下右移,这个卡了一下。最开始我还想用一个切片还存储当前满足条件的子串,后来发现是多么的愚蠢,因为这样的话我每次去判断在当前子串是否有string[right]以及对于后续的处理都会非常的麻烦 - 关于
left应该什么情况下右移,这里卡了比较长的时间。我最开始并没有考虑到需要判断当前map中string[right]的index和left的情况,只是想着如果有的map中有string[right]就直接把left挪到index就行了,这样实际会有可能把left往左移的,所以还是需要判断index和left的情况的;另外就是left和index判断的时候,最开始是left=index的,也是没有考虑完全,其实是需要left=index+1的。
这题在看到时间复杂度要求是O(log(m+n))的时候,是想过用二分法的,但是后续就没有思路了。
关于题解中给出的方法,这里说一下自己的理解过程,所谓中位数就是找到合并后的数组的第K个数,但是又不能真的合并了之后再去找,所以题解中的方法是从AB两个数组中每次删除K/2个数,同时需要比较AB数组中哪个更小,因为小的那个肯定是不满足条件的,但是大的那个数组就可能删过了。
func findMedianSortedArrays(nums1 []int, nums2 []int) float64 {
totalLength := len(nums1) + len(nums2)
if totalLength%2 == 1 {
midIndex := totalLength / 2
return float64(getKthElement(nums1, nums2, midIndex+1))
} else {
midIndex1, midIndex2 := totalLength/2-1, totalLength/2
return float64(getKthElement(nums1, nums2, midIndex1+1)+getKthElement(nums1, nums2, midIndex2+1)) / 2.0
}
}
func getKthElement(nums1, nums2 []int, k int) int {
index1, index2 := 0, 0
for {
if index1 == len(nums1) {
return nums2[index2+k-1]
}
if index2 == len(nums2) {
return nums1[index1+k-1]
}
if k == 1 {
return min(nums1[index1], nums2[index2])
}
half := k / 2
// 有一点不明白的就是这里为什么要加half之后再减1,我尝试改成了min(index1+half, len(nums1)-1)就报错了
// 明白了,这个是因为我既然要找第K个,那么AB两个前面必须都是K/2-1个,如果都是K/2个,那么就不满足第K个元素前面有K个,所以需要-1
newIndex1 := min(index1+half, len(nums1)) - 1
newIndex2 := min(index2+half, len(nums2)) - 1
pivot1, pivot2 := nums1[newIndex1], nums2[newIndex2]
if pivot1 <= pivot2 {
// 至于这里为什么需要+1是因为这样的话这样才等于k/2,可以把newIndex1=index1+k/2-1代入(不考虑越界的情况)
k -= (newIndex1 - index1 + 1)
// 这里为什么需要再加1,是因为newIndex1这个元素已经被排除了
index1 = newIndex1 + 1
} else {
k -= (newIndex2 - index2 + 1)
index2 = newIndex2 + 1
}
}
}
func min(x, y int) int {
if x < y {
return x
}
return y
}这题最开始也能想到把问题才小往大走,但是不知道原来这种做法叫做动态规划,这个有一个很重要的特点是会用空间换时间,也就是这里把最初的状态都记录下来:
var dp [1000][1000]bool
for i := range s {
dp[i][i] = true
}以及后续的这里,可以看到状态都被记录下来了。
if s[left] != s[right] {
dp[left][right] = false
} else {
if right-left < 3 {
dp[left][right] = true
} else {
dp[left][right] = dp[left+1][right-1]
}
}然后就是才小往大依次走就可以了,需要注意的下的是go写多了,不会写C#了,放下C#的二维数组
bool[,] dp = new bool[len, len];
for (int i = 0; i < len; i++)
{
dp[i,i] = true;
}这题自己最开始想到了第三种解法,就是按照最终的行,然后把一行一行拼起来,但是自己没有想到还能把每一行都分成很多周期
还有说下第二个循环那里为啥是j+i<len,因为这里的判断条件j+i就可以理解成当前节点
关于这题最开始又是非常的愚蠢,想着先转成字符串,然后再转回来那种写法,确实是太愚蠢了。
确实像题解里面的那个,我只要每次取得最后一个数就行了,就是判断是否越界的时候,不能在得到了新的数之后再去判断,要在这之前。说下题解中那个简单的判断是否越界的,那个是先算出来数之后再判断,根据是Java在越界后会强制设置为最大值/最小值,这里并不是对所有的语言都适用,需要注意。
这题基本都是自己的思路吧,就是要考虑的情况有点多,尤其是那个中间有空格的情况,我原本以为这种会直接跳过空格继续找呢,结果官方的意思是需要直接返回,算是我理解不到位的一个地方吧。
还有就是自己的rust水平,又忘的差不多了,系统的看了下字符串相关的知识,一定要记住String类型实际就是一个Vec<u8>,是一个utf-8类型的动态数组,至于那个&str就是切片,所以用索引例如s[0]这种实际访问并不一定能对应到一个有效的Unicode标量值,所以会报错,目前常用的操作如下
fn main() {
let s = String::from("中国人");
// 这里其实是可以看到c的类型是char,可以正确的输出中国人
for c in s.chars() {
println!("{}", c);
}
// 这里b的类型就是u8,所以输出的都是数字
for b in s.bytes() {
println!("{}", b);
}
}至于collect是将一个迭代器迭代的所有元素组合成一个新的集合,所以很多题目里面会有s.chars().collect(),就是将这个字符串转换过来成其他语言可以直接遍历的那种形式。
这题没有什么好说的,就是自己的笨方法转换成字符串然后再操作,其实复杂度还好
官方的解题方法是一种比较巧妙的可以把数字倒过来的办法,不过是只倒一半,不错不错
至于最后的x == reverted_number || x == reverted_number / 10这里前面没有什么说的,是偶数的情况,后面呢就是奇数的情况,不用考虑最后那个数字,这里还是比较巧妙的
首先恭喜下自己,能想到这种题应该用动态规划了,虽然还是没有做出来
其次说下和官方题目理解不一致的地方,官方的意思是假设s = "abcc" p = "abc*",是相当于*匹配了2次,而不是1次,如果匹配了0次的话,那么p = "ab",这里我感觉我的想法也是说的通的,只是和官方的本意不一致。
说下那个状态转移方程比较难以理解的地方,就是当p的最后一个字符是*且s[i]==p[j-1]的情况,f[i][j]=f[i-1][j]||f[i][j-2],前面的f[i-1][j]这里就是就是说的,我直接把s[i]舍弃掉,接着往前走就行了,后面那个或者f[i][j-2]的意思就是说,虽然s[i]==p[j-1]但是我也可以匹配0个,这两个只要有一个满足就行了,算是勉强理解了吧。
昨天被第10题吊打了之后,晚上看了一下这题,果然早上就有思路了。
这题最开始基本都能想到将两个坐标一个设置为0,一个设置为len-1,但是如何缩小这个范围, 也就是究竟是left++还是right--是一个非常需要考虑的问题,能想明白谁小就动谁就行了,因为只有动小的新面积才有可能更大,如果是动大的,新面积肯定小于等于现在的面积(因为小的限制了高,并且长变小了1)。
首先说下这题自己写出来也是没有问题,时间复杂度也还好,就是有点繁琐
关于题解的贪心法,自己刚开始也想到了,但是没有想到的这么巧妙,所以还是要多练习啊,加油。
基本都是自己的思路吧,还没有看题解,我觉得我的这个复杂度已经不错了,哈哈
Rust还是得练习啊,太菜了。
这题也是自己的想法就不错,没有看答案,哪天无聊再看看答案吧,应该也不能比我的更简洁了。
这题自己刚开始还想着把先走一遍遍历把数字放到map中,然后再像第一题那样,后来发现很难实现。
关于题解中需要理解的地方
- 排序之后如何去除重复的数是难点,也就是题解中的如果和前面一个数相等就继续走。
third--之后为什么在之后second的循环中不再设置为len-1?因为此时的数组已经是排序后的数组,second++之后,满足条件的third肯定是小于等于上次循环的third的,所以也就不需要再third = len-1
这题虽然最终的排名不行,但是自己的思路是完全正确的,复杂度也没有问题
说下自己当时写的时候不周到的地方,就是在确定了first的情况下,究竟是应该走second还是third的问题,最初的想法是谁变动下就动谁,这个是完全错误的
正确的确实是应该像后面写的那样,如果tempRes < target,就说明现在的结果还是太小了,应该让second++;同理如果tempRes > target,说明现在的值太大了,应该third--。
自己的想法问题也不大,只是没有这么优雅,也不知道这种方法叫做回溯法,并且这题的情况特殊,是并不需要提前返回的。
另外就是自己的Rust水平是真的烂啊,稍微复杂一点的情况就都写不了了,真是个弟弟。
还是先排序,然后要注意什么情况下可以接着走,还有就是如果答案正好的时候left和right应该怎么走,这两个数还是应该继续往中间走,因为中间还是有可能满足的情况的。
不过这题简直就是坑爹啊,本来难度也不是很难,做法和那个三数之和也有点类似,虽然还是看了下官方的题解,但是也差不多算掌握了,但是这个越界真的是把人折磨疯了,不知道有什么意义。
没什么说的,先计算下数量,然后倒过来删除就行了,就是需要注意下坐标。 文思泉涌,很快哈
自己的想法就是去实现一个栈,还想着如果可以的话用数字操作可能会更快,实际上并没有。另外以往自己写的Rust代码都没有体现Rust的风格,这次模仿着别人写的,以后尽量往这个上面靠拢。
fn main() {
let s = String::from("([)]");
let res = is_valid(s);
println!("{}", res);
}
fn is_valid(s: String) -> bool {
if s.len() % 2 == 1 {
return false;
}
let mut stack: Vec<char> = vec![];
for c in s.chars() {
match c {
'(' | '[' | '{' => stack.push(c),
')' => {
if stack.len() == 0 || stack.pop().unwrap() != '(' {
return false;
}
}
']' => {
if stack.len() == 0 || stack.pop().unwrap() != '[' {
return false;
}
}
'}' => {
if stack.len() == 0 || stack.pop().unwrap() != '{' {
return false;
}
}
_ => (),
}
}
stack.len() == 0
}自己的方法就是属于一直写,不够简洁,用递归的话确实就比较简单。另外Rust抄了一个别人的代码,看起来真的很好看。
impl Solution {
pub fn merge_two_lists(
list1: Option<Box<ListNode>>,
list2: Option<Box<ListNode>>,
) -> Option<Box<ListNode>> {
match (list1, list2) {
(Some(n1), Some(n2)) => {
if n1.val <= n2.val {
Some(Box::new(ListNode {
val: n1.val,
next: Solution::merge_two_lists(n1.next, Some(n2)),
}))
} else {
Some(Box::new(ListNode {
val: n2.val,
next: Solution::merge_two_lists(Some(n1), n2.next),
}))
}
}
(Some(n1), None) => Some(n1),
(None, Some(n2)) => Some(n2),
_ => None,
}
}
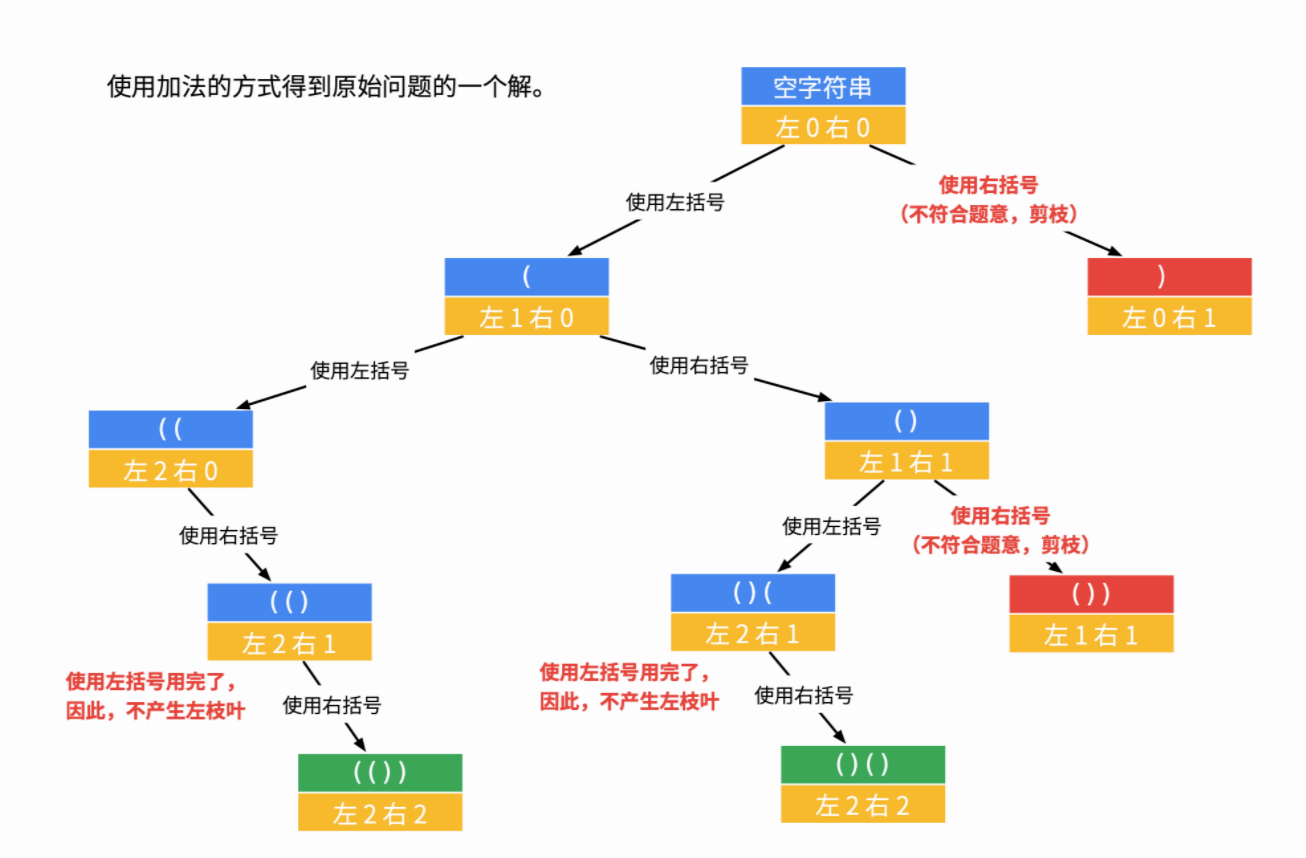
}这题自己原本写的是res = () + res || (res) || res + (),这样把这三个再拼成一个结果,然后再去重就行了,实际上自己是多么的愚蠢啊,这样会少一些情况,例如res = (())(),后面会有res = (())()()这种情况,就是插在了中间,所以就少考虑情况了。
放下别人的深度优先规划的解法
func generateParenthesis(n int) []string {
var res []string
generate(&res, "", 0, 0, n)
return res
}
func generate(res *[]string, str string, leftCount, rightCount, n int) {
if leftCount > n || rightCount > n || rightCount > leftCount {
return
}
if leftCount == n && rightCount == n {
*res = append(*res, str)
}
generate(res, str+"(", leftCount+1, rightCount, n)
generate(res, str+")", leftCount, rightCount+1, n)
}这题看到的第一时间就想到了第21题的两个有序链表,也确实可以那样做,就是两个两个合成,最终再返回就可以了。结果可以说是惨不忍睹,只击败了8%的兄弟。
痛,太痛了,改,改成不是两个两个合并的,是所有的一块合并,结果还是只击败了13%的人,还是看看大佬的吧。
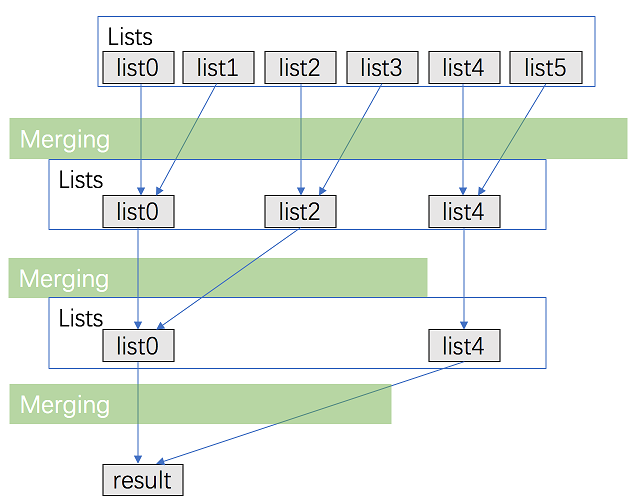
看了下官方的题解,第一种其实和我的一样,就是挨个合成,说下第二种分治合并
首先看下这个图,其实看下这个图就基本清楚了,其实就是在合并的时候不要再依次往后对比了,而是应该一直两个两个分,其实也就是二分的概念。
func mergeKLists(lists []*ListNode) *ListNode {
return merge(lists, 0, len(lists)-1)
}
func merge(lists []*ListNode, left, right int) *ListNode {
if left == right {
return lists[left]
}
if left > right {
return nil
}
mid := (left + right) / 2
return newMergeTwoLists(merge(lists, left, mid), merge(lists, mid+1, right))
}
func newMergeTwoLists(list1 *ListNode, list2 *ListNode) *ListNode {
if list1 == nil {
return list2
} else if list2 == nil {
return list1
} else if list1.Val <= list2.Val {
list1.Next = newMergeTwoLists(list1.Next, list2)
return list1
} else {
list2.Next = newMergeTwoLists(list1, list2.Next)
return list2
}
}这里放下根据这种思想写的go代码
还行,也没有什么卡壳的地方,很平稳的做出来了,思路就不写了,估计下次还是能做出来。
这题是一个困难题,不过自己也做出来,而且整体思路和官方题解的差别并不大,都是分为以下几步,先判断剩余的时候满足k,如果不满足的话就直接返回,如果满足的话就把剩余的翻转一下,其实自己写的问题就是翻转的过程写的太麻烦了,这里先放下官方的翻转过去,其中head和tail分别是首节点和尾节点:
public ListNode[] MyReverse(ListNode head, ListNode tail)
{
ListNode prev = tail.next;
ListNode p = head;
while (prev != tail)
{
ListNode nex = p.next;
p.next = prev;
prev = p;
p=nex;
}
return new ListNode[]{tail,head};
}关于这个算法,现在脑子已经有点晕了,先记录下,等会再去理解,先看书去了。
原本的做法是如果nums[left]==nums[right],就去找下一个不相等的nums[index],找到的话就把ritht--index都设置为nums[index],后来想了一下,根本没有必要,只需要把nums[right]设置为nums[index]就可以了。
**注意点一:**在设置了nums[right]=nums[index]之后需要注意不能再判断nums[left]==nums[right]了,因为有可能会出现nums[left]>nums[right]的情况,比如nums = {1,1,1,2,3,4},在第一次判断之后就会变成nums = {1,2,1,2,3,4},所以需要改变判断条件。
**注意点二:**可以提前退出,如果nums[left]==nums[len-1],就是说如果已经是满足条件的nums了,就可以提前返回结果了。
这里再说下官方题解,确实比我的巧妙多了:
pub fn remove_duplicates(nums: &mut Vec<i32>) -> i32 {
let len = nums.len();
if len <= 1 {
return len as i32;
}
let mut slow = 1; // slow是指下一次要更改值的坐标
let mut fast = 1; // fast是和前面不同的那个值,也就是将slow设置为fast
while fast < len {
if nums[fast] != nums[fast - 1] {
nums[slow] = nums[fast];
slow += 1;
}
fast += 1;
}
return slow as i32;
}其实这题我感觉不排序也可以做出来,不过那样应该比较麻烦,所以采取了排序的做法。
排序后,第一时间想的是采用二分法来找坐标,但是那样找到之后还需要再在附近找下其他坐标,感觉也挺麻烦的,直接依次递增了。
找到坐标后原本是采用确定这个范围,再来一个循环将这个范围内的值替换,后来看了下完全可以直接替换,就是需要退出的条件。
其他的这题就没有什么了,另外放下三种语言的排序,总是忘。
C#:array.sort(nums)Go:sort.Ints(nums)Rust:nums.sort_unstable()
自己的想法其实还行,看看效率什么的都还好,就是需要注意下在Rust中因为haystack_len和needle_len都是usize类型,所以在for i in 0..=haystack_len - needle_len之前需要判断大小,其他的就没啥了,放下三种语言取子串的区别:
C#:haystack.Substring(i, needleLength),这里的needleLength相当于长度Go:haystack[i:i+needleLen],这里相当于一个开闭区间Rust:&haystack[i..(i + needle_len)],这里和上面一样,都是一个开闭区间,需要注意下这里已经是&str之类的类型的
这题最开始的时候自己当去翻了下书,发现书里面并没有讲通过位运算来实现任意的除法,只有2的幂才可以,所以就想自己去写,后来写的时候就写不出来了,说下官方题解的思路。
- 先解决那些特殊情况
- 如果
dividend>divisor,那么这时结果是肯定大于1的,然后这个时候判断dividend是否大于2divisor,如果还大于就接着找,一直将后面的结果变大,如果超出的话,就用dividend-2ndivisor再和divisor比较,一直重复这个过程即可。
这题对自己还是有点难度的,并没有做出来,自己做的时候想的是直接得出words的所有组合,然后再依次的去比较,但是也没有写出来,当然这种方法的复杂度也是非常高的,下面说下自己对于官方题解的理解。
首先放下官方题解的全部内容,理解过程中花了时间的部分在代码中标注:
记 words 的长度为 wordsLen,words 中每个单词的长度为 wordLen,s的长度为sLen。首先需要将s划分为单词组,每个单词的大小均为wordLen(首尾除外)(虽然我说了有难以理解的地方在下面写,但是官方的这里真的写的很难理解,感觉把这句去掉更容易理解)。这样的划分方法有wordLen种,即先删去前i(i=0~wordLen-1)个字母后,将剩下的字母进行划分,如果末尾有不到wordLen个字母也删去。对这wordLen种划分得到的单词数组分别使用滑动窗口对words进行类似于「字母异位词」的搜寻。
划分成单词组后,一个窗口包含sLen中前wordsLen个单词,用一个哈希表differ表示窗口中单词频次和words中单词频次之差。初始化differ时,出现在窗口中的单词,每出现一次,相应的值增加1,出现在words中的单词,每出现一次,相应的值减少1。然后将窗口右移,右侧会加入一个单词,左侧会移出一个单词,并对differ做相应的更新。窗口移动时,若出现differ中值不为0的键的数量为0,则表示这个窗口中的单词频次和words中单词频次相同,窗口的左端点是一个待求的起始位置。划分的方法有wordLen种,做wordLen次滑动窗口后,即可找到所有的起始位置。
public IList<int> FindSubstring(string s, string[] words)
{
int sLen = s.Length;
int wordsLen = words.Length;
int wordLen = words[0].Length;
IList<int> result = new List<int>();
// 为什么这里是i<wordLen就可以了,是因为下面采用了滑动窗口,所有最初的起点只有0..wordLen-1这些位置就可以了
// 因为这个原因,所以下面的start每次递增都是wordLen
for (int i = 0; i < wordLen && i + wordsLen * wordLen <= sLen; i++)
{
// differ的作用,differ记录的是滑动窗口和words中每个单词出现的频次差,如果当前的滑动窗口和words中的频次差都为0
// 那么当前的滑动窗口就是满足条件的,将这个窗口的起点位置记录即可
Dictionary<string, int> differ = new Dictionary<string, int>();
// 这里是先确定一个起点为i,大小为wordsLen*wordLen的滑动窗口,并将s中i~i+wordsLen*wordLen的内容都放进differ
for (int j = 0; j < wordsLen; j++)
{
string word = s.Substring(i + j * wordLen, wordLen);
if (!differ.ContainsKey(word))
{
differ.Add(word, 0);
}
differ[word]++;
}
// 上一步已经将s中的内容放进去了,我们就可以比对和words中的差别了,如果有的就将这个减1即可
foreach (string word in words)
{
if (!differ.ContainsKey(word))
{
differ.Add(word, 0);
}
differ[word]--;
if (differ[word] == 0)
{
differ.Remove(word);
}
}
// 这里开始滑动这个窗口,每次滑动的步长都是wordLen
for (int start = i; start < sLen - wordsLen * wordLen + 1; start += wordLen)
{
// 因为start是从i开始的,所以这里要排除一下,其实可以再遍历了words之后就先判断i位置是否满足条件的
if (start != i)
{
// 窗口右滑的时候,右边新进入一个单词,把这个单词加入滑动窗口的differ中
// 注意这里是start+(wordsLen-1)*wordLen,并不是start+wordsLen*wordLen
// 因为这个时候start已经是i+wordLen了,即start已经不是原滑动窗口的下标了
// 而是新的滑动窗口的下标
string word = s.Substring(start + (wordsLen - 1) * wordLen, wordLen);
if (!differ.ContainsKey(word))
{
differ.Add(word, 0);
}
differ[word]++;
if (differ[word] == 0)
{
differ.Remove(word);
}
// 窗口右滑的时候,左边要出去一个单词,将这个单词从differ中去除
// 这里的start-wordLen和上面同理,start是新的滑动窗口的下标
word = s.Substring(start - wordLen, wordLen);
if (!differ.ContainsKey(word))
{
differ.Add(word, 0);
}
differ[word]--;
if (differ[word] == 0)
{
differ.Remove(word);
}
}
// 如果这个滑动窗口中所有的都没有差异,那么这个滑动窗口的开始下标就是答案之一
if (differ.Count == 0)
{
result.Add(start);
}
}
}
return result;
}挖个坑,明天先写Rust版本的题解,看看还掌握多少,另外一定要坚持写Rust,已经重新学几次了。
自己最开始想的是如果后面的序列等于不等于倒序排列的最大值的话就继续往后面排,但是被空间复杂度给限制了,此题只允许用少量常数,关键我还想了很长时间,只能看答案了。
题解中的意思是我从后往前找,找到第一个比前面小的值left,然后再从后面往前找,找到第一个比left大的值right,之后将这两个值对调,那么现在从left+1往后的序列就是从大到小排列的,只需要再将后面这些倒序就可以了
注意:这里的left和right是我最初的理解,我以为第一个数的坐标肯定在左边,其实并不是,这两个可以是数组中的任意位置
pub fn next_permutation(nums: &mut Vec<i32>) {
let len = nums.len() as i32;
let mut left = len - 2;
let mut right = len - 1;
// 找到left
while left >= 0 && nums[left as usize] >= nums[left as usize + 1] {
left -= 1;
}
// 如果找到的left已经太靠前了,已经越界了,说明当前的数组就是所有排列里面最后的一个了
if left >= 0 {
// 找到right,这里的right就是从后往前找第一个大于left的值
// 需要注意这里的right并不一定需要在left的右边
while right >= 0 && nums[left as usize] >= nums[right as usize] {
right -= 1;
}
// 经过对调的left之后的数组一定是从大到小排列的
// LeetCode的网站上面不支持这种方式,实际是vscode是可以的
(nums[left as usize],nums[right as usize]) = (nums[right as usize],nums[left as usize]);
}
// 注意这里重新排列的起始坐标是left+1,因为正常情况下这里的left已经是原本的right的值对调了
// 也就是说最开始的值已经变成原本的下一位,因为left之后的已经是从大到小排列的了,所以倒序即可
reverted_nums(nums, left as usize + 1)
}
pub fn reverted_nums(nums: &mut Vec<i32>, mut left: usize) {
let mut right = nums.len() - 1;
while left < right {
(nums[left as usize],nums[right as usize]) = (nums[right as usize],nums[left as usize]);
left += 1;
right -= 1;
}
}疑问:我在Rust中通过与或交换两个数的值,结果不知道是否因为在数组中,导致出现了原本不存在的值,所以有点疑惑,下次需要注意下
第一时间想到了动态规划,但是自己刚开始想到是用dp[left][right]存放bool类型来表示当前的的区间是否满足要求,之后再想办法得到下一个状态,实际是错误的。
官方题解的做法是dp[index]来表示截止到当前坐标的满足条件的最大值,之后再判断下一个的状态。
pub fn longest_valid_parentheses(s: String) -> i32 {
let mut res = 0;
let mut dp:Vec<usize> = vec![0;s.len()];
let s: Vec<char> = s.chars().collect();
for i in 1..s.len() {
// 如果下一个是'('就跳过,肯定不满足
if s[i] == ')' {
// 如果前一个是'(',说明这两个直接满足了,dp[i]=dp[i-2]+2
if s[i - 1] == '(' {
// 需要注意下i<2时数组越界的情况
if i >= 2 {
dp[i] = dp[i - 2] + 2;
} else {
dp[i] = 2;
}
// 如果当前dp[i-1]开始坐标的前面一个是`(`,那么就和现在的这个`)`配对上了
} else if i - dp[i - 1] > 0 && s[i - dp[i - 1] - 1] == '(' {
// 考虑下dp[i-1]开始坐标的前面也满足条件,原本因为开始坐标前面的一个`(`导致连续断了,
// 现在这个`(`又dp[i]可以用的了,那么就需要再加上`dp[i-dp[i-1]-2]`了
if i - dp[i - 1] >= 2 {
dp[i] = dp[i - 1] + dp[i - dp[i - 1] - 2] + 2;
} else {
dp[i] = dp[i - 1] + 2;
}
}
if dp[i] > res {
res = dp[i];
}
}
}
res as i32
}这题的重点就是每次将数组分开之后都会有一个数组是排序的,一个和原本一样是没有排序好的,然后再看target是否在排序好的这个区间里面,如果不在话就在另外一个里面
pub fn search(nums: Vec<i32>, target: i32) -> i32 {
let len = nums.len();
if len == 1 {
if nums[0] == target {
return 0;
} else {
return -1;
}
}
let mut left = 0;
let mut right = len - 1;
while left <= right {
let mid = (left + right) / 2;
if nums[mid] == target {
return mid as i32;
}
// 判断mid之前的数组是否是排序好的,如果不是的话就在mid之后
if nums[0] <= nums[mid] {
// 判断target是否满足mid之前排序好的数组,如果不满足说明在mid后面
if nums[0] <= target && target <= nums[mid] {
right = mid - 1;
} else {
left = mid + 1;
}
} else {
// 判断target是否满足mid之后排序好的数组,如果不满足说明在mid前面
if nums[mid] <= target && target <= nums[len - 1] {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
-1
}因为题目已经要求时间复杂度是O(log n)所以我直接一个二分法的做,果然哈,很快,一个小时不到三种写法写完,美滋滋
你问我官方的方法是不是更简单,这我就不知道了,因为我直接一个不看
pub fn search_range(nums: Vec<i32>, target: i32) -> Vec<i32> {
let mut left: i32 = 0;
let mut right: i32 = nums.len() as i32 - 1;
while left <= right {
let mid = (left + right) / 2;
if nums[mid as usize] == target {
let mut begin = mid;
let mut end = mid;
while begin > 0 && nums[begin as usize - 1] == target {
begin -= 1;
}
while end < nums.len() as i32 - 1 && nums[end as usize + 1] == target {
end += 1;
}
return vec![begin, end];
} else if nums[mid as usize] < target {
left = mid + 1;
} else {
right = mid - 1;
}
}
return vec![-1, -1];
}也是直接二分,无需多言,附上我的战绩及优美代码,要是所有题都能做这么快就好了。
pub fn search_insert(nums: Vec<i32>, target: i32) -> i32 {
let mut left = 0;
let mut right = nums.len() - 1;
while left <= right {
if target < nums[left] {
return left as i32;
} else if target > nums[right] {
return right as i32 + 1;
} else {
let mid = (left + right) / 2;
if target < nums[mid] {
right = mid - 1;
} else if target > nums[mid] {
left = mid + 1;
} else {
return mid as i32;
}
}
}
0
}自己的解法和官方的差不多,基本都是先横着找再竖着找,然后小方块小方块的找,找到之后判断这个是否符合数独的要求,over。
看了下一题的题目,我估计我要看答案了。
果然这题是直接看的答案,而且还没有去理解,不知道为啥就是不想做这题,先这样吧。
这题没有什么需要特别说的,思想基本都差不多,其实都是递归,官方的题解就是没有再写一个方法
另外通过这题知道了有一种方式叫做打表,就是先把所有的答案都写出来。
自己的想法是贪心+递归从后往前找,但是这种情况下有导致有些数值被跳过去,下面说下针对官方题解的理解。
这题官方的题解感觉不如网友“liweiwei1419”的清晰,这里说下关于这个题解的理解:
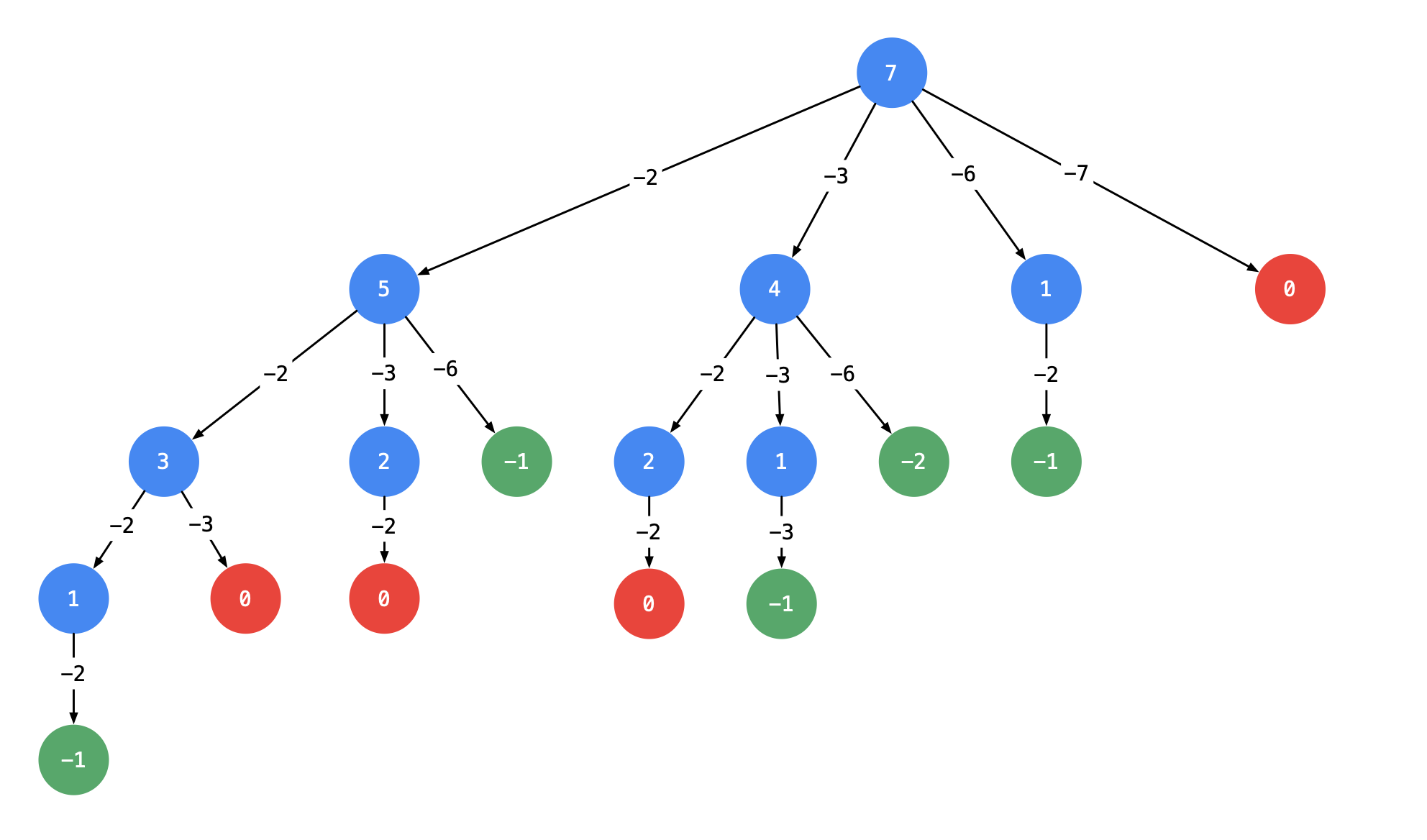
考虑情况candidates = [2, 3, 6, 7],target=7:
- 当第一个数字是
2,如果找到后续的总和为7-2=5的所有组合,再在前面加上2,就是第一个是2的所有满足条件的组合 - 当第一个数字是
3,同理找到组合为7-3=4的所有组合,再在前面加上3,就是第一个数字是3的所有满足条件的组合
基于以上的想法,可以画出如下树形图:
说明:
- 以
target=7为根节点,创建一个分支时做减法; - 每一个箭头表示:从父节点的数值减去边上的数值,得到子节点的数值。边的值就是题目中给出的
candidate数组的每个元素的值; - 减到
0或者负数的时候停止,即:节点0和负数节点成为子节点; - 所有从根节点到节点
0的路径(只能从上往下,没有回路)就是题目中要找的一个结果。
这棵树有4个子节点的值为0,对应的路径是[2,2,3],[2,3,2],[3,2,2],[7],可以看到有重复的了。
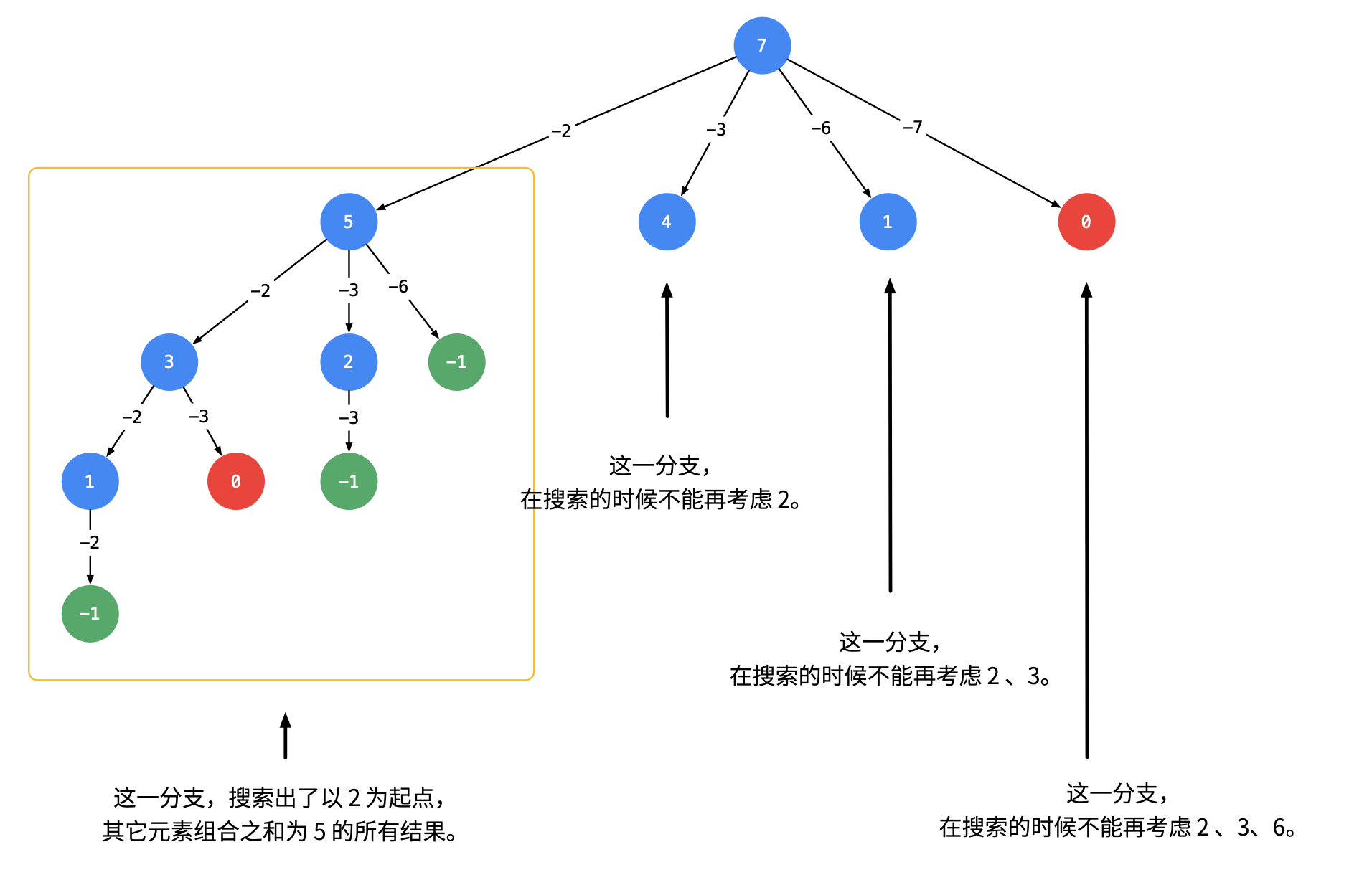
思考为什么会产生重复,其实就是因为假如我在以3为第一个结果的时候,还添加了2,实际上这个已经添加过了。那么为了解决这个问题,包括在之后的不计算顺序的问题的时候,我们可以在搜索的时候按照某种顺序搜索。具体的做法就是:每一次搜索的时候设置下一轮搜索的起点begin,如下图:
即:从每一层的第2个节点开始,都不能再搜索产生同一层节点已经使用过的candidate里的元素,这里放下根据这种思路写的C#代码
public class Solution
{
public IList<IList<int>> CombinationSum(int[] candidates, int target)
{
int len = candidates.Length;
IList<IList<int>> res = new List<IList<int>>();
if (len == 0)
{
return res;
}
Stack<int> path = new Stack<int>();
dfs(candidates, 0, len, target, path, res);
return res;
}
public void dfs(int[] candidates, int begin, int len, int target, Stack<int> path, IList<IList<int>> res)
{
if (target < 0)
{
return;
}
if (target == 0)
{
res.Add(new List<int>(path));
return;
}
for (int i = begin; i < len; i++)
{
path.Push(candidates[i]);
dfs(candidates, i, len, target - candidates[i], path, res);
path.Pop();
}
}
}这题和上面一题有一点相似,但是要求不能有重复的组合,通过以下两步就可以做到
public class Solution
{
public IList<IList<int>> CombinationSum2(int[] candidates, int target)
{
int len = candidates.Length;
IList<IList<int>> res = new List<IList<int>>();
if (len == 0)
{
return res;
}
// 首先是这里的需要对这个数组进行排序,为了下一步做准备
Array.Sort(candidates);
Stack<int> path = new Stack<int>();
Dsf2(candidates, 0, len, target, path, res);
return res;
}
public void Dsf2(int[] candidates, int begin, int len, int target, Stack<int> path, IList<IList<int>> res)
{
if (target == 0)
{
List<int> newPath = new(path);
newPath.Sort();
res.Add(newPath);
return;
}
for (int i = begin; i < len; i++)
{
if (target - candidates[i] < 0)
{
break;
}
// 这一步的剪枝,就是如果这个数并不是开始的第一个数,并且这个数和前面的那一个相同就说明这个组合是重复的
if (i > begin && candidates[i] == candidates[i - 1])
{
continue;
}
path.Push(candidates[i]);
Dsf2(candidates, i + 1, len, target - candidates[i], path, res);
path.Pop();
}
}
}只能说困难题不愧是困难题啊,是真的不会做啊,说下官方题解的理解吧。
本题的难点在于对于空间复杂度的要求,如果没有要求的话完全可以用一个哈希表把这个数字是否出现存下来,然后遍历一遍就行了,现在的方法就是在原有数组上实现一个类型哈希表的结果,来记录当前的数是否出现过。
- 首先明确一点,对于一个长度为
len的数组,最终的结果一定是在1~len+1之间,这一点比较容易想明白 - 对于那些
nums[i]<=0的数,可以直接把这个数设置为一个len+1,这里设置成什么是无所谓的,只要大于len即可,反正也不会用到 - 这一步是关键:如果
nums[i]<=len,那么就表示这个数字出现在了1~len+1这个区间内了,那么我就将第nums[i]-1设置打上标记,题解中的打标记采用的是取负数的方式,第一要注意,这里的nums[i]-1是新的坐标,这个坐标一定在nums的范围内的,这样当判断nums[i]<=0时,就可以知道i+1这个数在nums中出现过 - 还有一些细节,就是在第3步中每次取
nums[i]的时候,这个数可以因为前面的数导致变成负数了,所以在每次取之前需要都取一下绝对值 - 最终再来一次遍历,我们找到第一个
nums[i]>0的即可,这样就表示i+1这个数没有出现过并且1~i都出现了,如果都出现了我们就返回len+1即可。
class Solution
{
public:
int firstMissingPositive(vector<int> &nums)
{
int len = nums.size();
//
for (int i = 0; i < len; i++)
{
if (nums[i] <= 0)
{
nums[i] = len + 1;
}
}
for (int i = 0; i < len; i++)
{
int num = abs(nums[i]);
if (num <= len)
{
// 这里需要注意下,新的坐标是num-1
nums[num - 1] = -abs(nums[num - 1]);
}
}
for (int i = 0; i < len; i++)
{
if (nums[i] > 0)
{
return i + 1;
}
}
return len + 1;
}
};这题其实自己是做出来的,但是超时了,这里把自己的做法和官方的做法都放一下
// 自己的做法的中心思想就是一行一行算,然后计算这一行符合条件的值
func trap(height []int) int {
res := 0
begin := 0
end := len(height) - 1
maxDiffer := 0
for i := 0; i < len(height); i++ {
if height[i] > maxDiffer {
maxDiffer = height[i]
}
}
for differ := 0; differ < maxDiffer-1; differ++ {
begin, end = getNewBeginAndEnd(height, differ, begin, end)
lineRes := 0
for index := begin + 1; index < end; index++ {
if height[index]-differ <= 0 {
lineRes++
}
}
res += lineRes
}
return res
}
func getNewBeginAndEnd(height []int, differ, oldBegin, oldEnd int) (int, int) {
var newBegin, newEnd int
for newBegin = oldBegin; newBegin < oldEnd; newBegin++ {
if height[newBegin]-differ > 0 {
break
}
}
for newEnd = oldEnd; newEnd > oldBegin; newEnd-- {
if height[newEnd]-differ > 0 {
break
}
}
return newBegin, newEnd
}官方接法->动态规划(DP)
public int Trap(int[] height)
{
int res = 0;
int len = height.Length;
if (len == 0) return 0;
// leftMax表示当前坐标的左边的最大值
int[] leftMax = new int[len];
leftMax[0] = height[0];
for (int i = 1; i < len; i++)
{
leftMax[i] = Math.Max(leftMax[i-1],height[i]);
}
int[] rightMax = new int[len];
// rightMax表示当前坐标右边的最大值
rightMax[len - 1] = height[len - 1];
for (int i = len - 2; i >= 0; i--)
{
rightMax[i] = Math.Max(rightMax[i+1],height[i]);
}
for (int i = 0; i < len; i++)
{
// leftMax[i]和right[i]的较小值减去当前坐标值就是当前坐标能盛放的雨水
res += Math.Min(leftMax[i],rightMax[i]) - height[i];
}
return res;
}自己也写了一版,但是会有i32越界的问题,这里说下官方的两种解法
第一种,模拟乘法的过程
这种方法其实就是用第一个字符串依次倒叙乘以第二个的数,然后再实现一个字符串的加法
func multiply(num1 string, num2 string) string {
if num1 == "0" || num2 == "0" {
return "0"
}
res := "0"
len1, len2 := len(num1), len(num2)
for i := len2 - 1; i >= 0; i-- {
curr := ""
add := 0
for j := len2 - 1; j > i; j-- {
curr += "0"
}
y := int(num2[i] - '0')
for j := len1 - 1; j >= 0; j-- {
x := int(num1[j] - '0')
product := x*y + add
curr = strconv.Itoa(product%10) + curr
add = product / 10
}
for ; add != 0; add /= 10 {
curr = strconv.Itoa(add%10) + curr
}
res = addStrings(res, curr)
}
return res
}
func addStrings(num1 string, num2 string) string {
index1, index2 := len(num1)-1, len(num2)-1
add := 0
res := ""
for ; index1 >= 0 || index2 >= 0 || add != 0; index1, index2 = index1-1, index2-1 {
x, y := 0, 0
if index1 >= 0 {
x = int(num1[index1] - '0')
}
if index2 >= 0 {
y = int(num2[index2] - '0')
}
tempRes := x + y + add
res = strconv.Itoa(tempRes%10) + res
add = tempRes / 10
}
return res
}第二种,其实也是乘法的过程
这种方法是:
- 先用一个
len1+len2的数组来盛放所有的内容,为什么是len1+len2是因为一个len1的数组乘以一个len2的数组的新答案肯定小于等于len1+len2, - 将
num1[i]*num2[j]的数字相乘放在新数组的i+j+1这个位置,至于为什么是这个位置需要好好的观察一下 - 之后将新数组的按照十进制的方式整理下即可,注意这里最前面可能是
0,记得舍弃掉
class Solution {
public String multiply(String num1, String num2) {
if (num1.equals("0") || num2.equals("0")) {
return "0";
}
StringBuilder res = new StringBuilder();
int len1 = num1.length();
int len2 = num2.length();
int[] resArr = new int[len1 + len2];
for (int i = len1 - 1; i >= 0; i--) {
int x = num1.charAt(i) - '0';
for (int j = len2 - 1; j >= 0; j--) {
int y = num2.charAt(j) - '0';
resArr[i + j + 1] += x * y;
}
}
for (int i = len1 + len2 - 1; i > 0; i--) {
resArr[i - 1] += resArr[i] / 10;
resArr[i] %= 10;
}
int begin = resArr[0] == 0 ? 1 : 0;
for (int i = begin; i < len1 + len2; i++) {
res.append(resArr[i]);
}
return res.toString();
}
}这题和前面一个匹配其实差不多,都是直接用动态规划的方法就可以了。当然了,我还是没有做出来
impl Solution {
pub fn is_match(s: String, p: String) -> bool {
let s = s.chars().collect::<Vec<char>>();
let p = p.chars().collect::<Vec<char>>();
let (len_s, len_p) = (s.len(), p.len());
let mut dp = vec![vec![false; len_p + 1]; len_s + 1];
dp[0][0] = true;
// 因为*是可以直接舍弃的,所以无论p前面有多少个*,dp[0][i]都是true
for i in 1..=len_p {
if p[i - 1] == '*' {
dp[0][i] = true;
} else {
break;
}
}
for i in 1..=len_s {
for j in 1..=len_p {
// 这里的*,如果不使用*的话,那么dp[i][j]=dp[i][j-1]
// 如果使用*的话,那么dp[i][j]=dp[i-1][j]
if p[j - 1] == '*' {
dp[i][j] = dp[i][j - 1] || dp[i - 1][j];
} else if p[j - 1] == '?' || s[i - 1] == p[j - 1] {
dp[i][j] = dp[i - 1][j - 1];
}
}
}
dp[len_s][len_p]
}
}贪心算法,确定本次跳的范围内可以跳的最远的一个就是新的起点就行了。
impl Solution {
pub fn jump(nums: Vec<i32>) -> i32 {
let len = nums.len();
let mut count = 0;
let mut begin = 0;
while begin <= len - 1 {
if begin == len - 1 {
break;
} else if begin + nums[begin] as usize >= len - 1 {
count += 1;
break;
} else {
let mut temp = 0;
let mut new_begin = begin;
for i in 1..=nums[begin] as usize {
if temp <= nums[begin + i] + i as i32 {
temp = nums[begin + i] + i as i32;
new_begin = begin + i;
}
}
count += 1;
begin = new_begin;
}
}
count
}
}以下内容来源
以下是维基百科中「回溯算法」和「深度优先遍历」的定义。
回溯法: 采用试错的思想,它尝试分步的去解决一个问题。在分步解决问题的过程中,当它通过尝试发现现有的分步答案不能得到有效的正确的解答的时候,它将取消上一步甚至是上几步的计算,再通过其它的可能的分步解答再次尝试寻找问题的答案。回溯法通常用最简单的递归方法来实现,在反复重复上述的步骤后可能出现两种情况:
- 找到一个可能存在的正确的答案;
- 在尝试了所有可能的分步方法后宣告该问题没有答案。
深度优先搜索算法:(英语:Depth-First-Search,DFS)是一种用于遍历或搜索树或图的算法。这个算法会尽可能深的搜索树的分支。当节点v的所在边都己被探寻过,搜索将回溯到发现节点v的那条边的起始节点。这一过程一直进行到已发现从源结点可达的所有节点为止。如果还存在未被发现的节点,则选择其中一个作为源节点并重复以上过程,整个进程反复进行直到所有节点都被访问为止。
回溯算法与深度优先遍历都有不撞南墙不回头的意思。我个人的理解是:回溯算法强调了深度优先遍历思想的用途,用一个不断变化的变量,在尝试各种可能的过程中,搜索需要的结果。强调了回退操作对于搜索的合理性。而深度优先遍历强调一种遍历的思想,与之对应的遍历思想是广度优先遍历。至于广度优先遍历为什么没有成为强大的搜索算法,我们在题解后面会提。
我们每天使用的搜索引擎帮助我们在庞大的互联网上搜索信息。搜索引擎的搜索和回溯搜索算法里搜索的意思是一样的。
搜索问题的解,可以通过遍历实现。所以很多教程把回溯算法称为爆搜(暴力解法)。因此回溯算法用于搜索一个问题的所有的解,通过深度优先遍历的思想实现。
共同点
用于求解多阶段决策问题。多阶段决策问题即:
- 求解一个问题分为很多步骤(阶段);
- 每一个步骤(阶段)可以有多种选择。
不同点
- 动态规划只要求我们评估最优解是多少,最优解对应的具体解是什么并不要求。因此很适合应用于评估一个方案的效果;
- 回溯算法可以搜索得到所有的方案(当然包括最优解),但是本质上它是一种遍历算法,时间复杂度很高。
我们以数组[1,2,3]的全排列为例:
- 先写以
1开头的全排列,它们是[1,2,3],[1,3,2],即1+[2,3]的全排列(注意:递归结构体现在这里); - 再写以
2开头的全排列,它们是[2,1,3],[2,3,1],即2+[1,3]的全排列; - 最后写以
3开头的全排列,它们是[3,1,2],[3,2,1],即3+[1,2]的全排列。
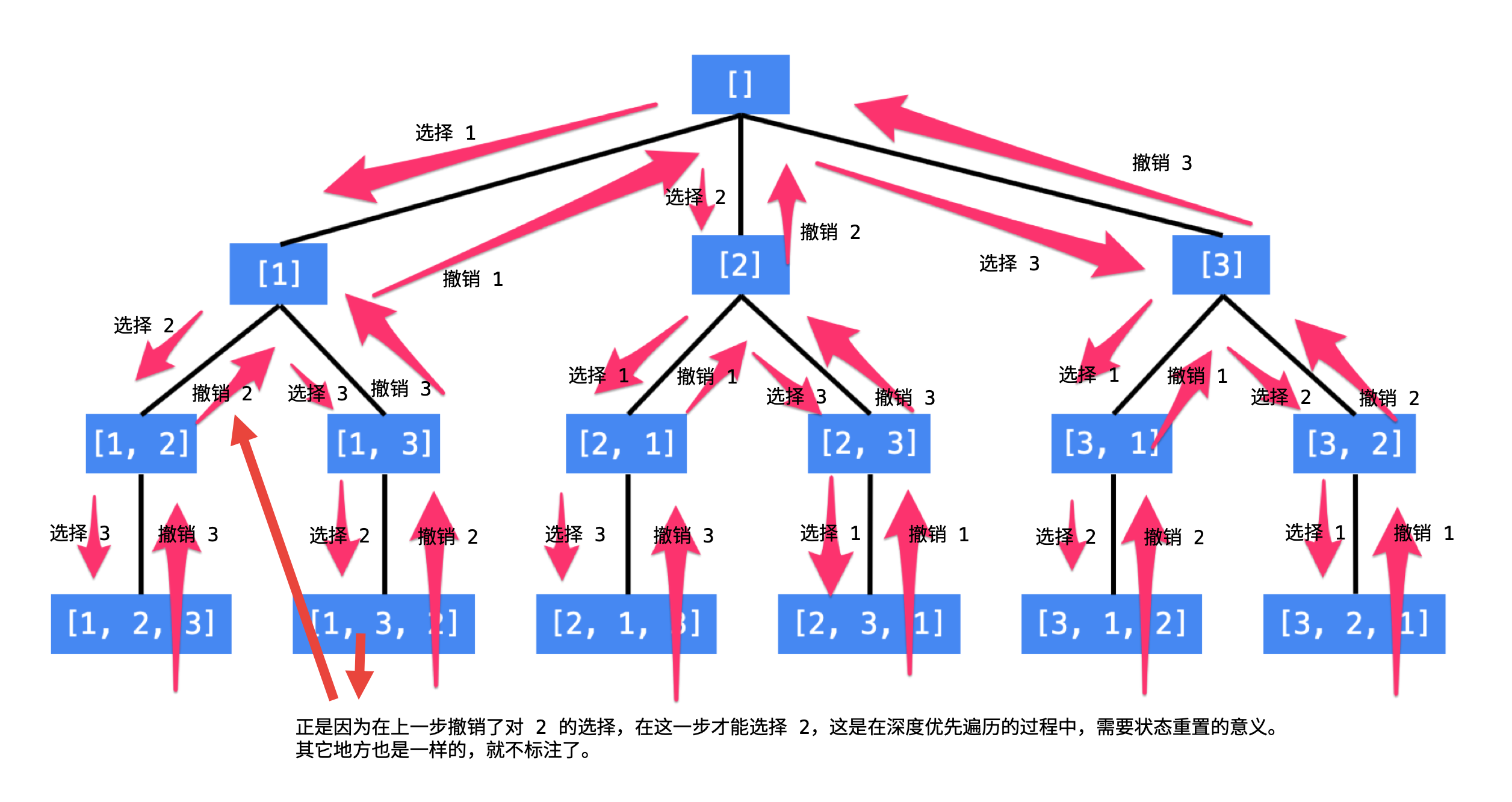
总结搜索的方法:按顺序枚举每一位可能出现的情况,已经选择的数字在当前要选择的数字中不能出现。按照这种策略搜索就能做到不重不漏。这样的思路,可以用一个树形结构表示。
说明:
- 每一个节点表示了求解全排列问题的不同阶段,这些阶段通过变量的不同的值体现,这些变量的不同的值,称之为状态;
- 使用深度优先遍历有回头的过程,在回头以后,状态变量需要设置成和先前一样,因此在回到上一层节点的过程中,需要撤销上一次的选择,这个操作称之为状态重置;
- 深度优先变量,借助系统栈空间,保存所需要的状态变量,在编码中只需要注意遍历到相应的节点的时候,状态变量的值是正确的,具体的做法是:往下走一层的时候,
path变量在尾部追加,而往回走的时候,需要撤销上一次的选择,也是在尾部操作,因此path变量是一个栈; - 深度优先遍历是通过回溯操作,实现了全局使用一份状态变量的效果。
使用编程的方法得到全排列,就是在这样的一个树形结构中完成遍历,从树的根节点到叶子节点形成的路径就是其中的一个全排列。
- 首先这棵树除了根节点和叶子节点以外,每一个节点所做的事情都是一样的,即:在已经选择了一些数的前提下,在剩下的还没有选择的数中,依次选择一个数,这显然是一个递归结构;
- 递归的终止条件是:一个排列中的数字已经选够了,因此我们需要一个变量来表示当前程序递归到了第几层,我们把这个变量叫做
depth,或者命名为index,表示当前要确定是某个全排列中下标为index的那个数是多少;(其实这里是不需要这个变量的,我们直接取上面那个栈path的长度就可以了) - 布尔数组
used,初始化的时候都为false表示这些数还没有被选择,当我们选定一个数的时候,就将这个数组的相应位置设置为true,这样在考虑下一个位置的时候,就能够以$O(1)$的时间复杂度判断这个数是否被选择过,这是一种以空间换时间的思想。
这些变量称为状态变量,它们表示了在求解一个问题的时候所处的阶段,需要根据问题的场景设计合适的状态变量。
public class Solution
{
public IList<IList<int>> Permute(int[] nums)
{
List<IList<int>> res = new();
int len = nums.Length;
if (len == 0) return res;
bool[] used = new bool[len];
Stack<int> path = new Stack<int>(len);
Dfs(nums, path, used, res);
return res;
}
private void Dfs(int[] nums, Stack<int> path, bool[] used, List<IList<int>> res)
{
if (path.Count == nums.Length)
{
res.Add(new List<int>(path));
return;
}
for (int i = 0; i < nums.Length; i++)
{
if (used[i]) continue;
path.Push(nums[i]);
used[i] = true;
Dfs(nums, path, used, res);
used[i] = false;
path.Pop();
}
}
}和上面一题差别不大,就是需要想明白怎么才能避免重复,其实就是已经排序的情况下加下面的一句:
if i > 0 && nums[i] == nums[i - 1] && !used[i - 1] {
continue;
}最前面的i>0没有什么好说的,后面的nums[i]==nums[i-1]就是判断当前的元素是否和前面一个元素相同,但是这样还不够,我们需要考虑的是同一层的相同值已经被使用的情况。假如nums=[1,1,2],path[0]=1,我们并不能简单的将这种情况剪枝,所以就需要判断used[i-1],如果是true的情况下就说明第二个1处于下一层,也就是可以用,反之如果used[i-1]=false的情况下这个数字就不能用了,直接剪枝。
真的挺绕的,继续加油。
没有什么要说的,就是找到这个位置的数字应该在哪里出现就行了,然后挨个换,需要注意的就是确定i和j的范围
class Solution {
public void rotate(int[][] matrix) {
int len = matrix.length;
if (len == 1) {
return;
}
int temp1, temp2, temp3, temp4;
// 这里的i不用走完,只要走一半就行了
for (int i = 0; i < (len + 1) / 2; i++) {
// 这里的j是最开始走多,越到后面走的越少
for (int j = i; j < len - i - 1; j++) {
temp1 = matrix[i][j];
temp2 = matrix[j][len - i - 1];
temp3 = matrix[len - i - 1][len - j - 1];
temp4 = matrix[len - j - 1][i];
matrix[i][j] = temp4;
matrix[j][len - i - 1] = temp1;
matrix[len - i - 1][len - j - 1] = temp2;
matrix[len - j - 1][i] = temp3;
}
}
return;
}
}写了两种方法,第一种很省内存,但是时间复杂度较高;第二种就是用内存换时间了。
class Solution {
public:
vector<vector<string>> groupAnagrams1(vector<string> &strs) {
vector<vector<string>> res;
int len = strs.size();
if (len == 1) {
res.push_back(strs);
return res;
}
vector<bool> used = vector<bool>(len, false);
vector<string> tempRes;
string tempI;
string tempJ;
for (int i = 0; i < len; i++) {
if (used[i]) {
continue;
}
tempRes.push_back(strs[i]);
used[i] = true;
tempI = strs[i];
int lenI = tempI.length();
sort(tempI.begin(), tempI.end());
for (int j = i + 1; j < len; j++) {
if (used[j] || lenI != strs[j].length()) {
continue;
}
tempJ = strs[j];
sort(tempJ.begin(), tempJ.end());
if (tempI == tempJ) {
tempRes.push_back(strs[j]);
used[j] = true;
}
}
res.push_back(tempRes);
tempRes.clear();
}
return res;
}
// 这里就是将组成相同相同的用unordered_map存起来就行了
vector<vector<string>> groupAnagrams2(vector<string> &strs) {
vector<vector<string>> res;
int len = strs.size();
if (len == 1) {
res.push_back(strs);
return res;
}
unordered_map<string, vector<string>> hashMap;
string tempStr;
for (int i = 0; i < len; i++) {
tempStr = strs[i];
sort(tempStr.begin(), tempStr.end());
if (hashMap.find(tempStr) == hashMap.end()) {
hashMap.insert(pair<string, vector<string>>(tempStr, vector<string>{strs[i]}));
} else {
hashMap[tempStr].push_back(strs[i]);
}
}
for (const auto &item: hashMap) {
res.push_back(item.second);
}
return res;
}
};看到这题的第一时间想到的是那个自己实现除法的问题,其实自己的做法也一样,不过官方题解的大概看起来会更简洁一点,不过我还是更喜欢自己的解法,比较容易理解,这里都放下:
pub fn my_pow(x: f64, n: i32) -> f64 {
if n >= 0 {
return my_quick_mul(x, n);
}
return 1.00000 / my_quick_mul(x, -n);
}
// 官方解法,这种确实自己想不起来,就是在那个为奇数的时候乘以x,确实可以满足所有数
pub fn quick_mul(x: f64, n: i32) -> f64 {
if n == 0 {
return 1.00000;
}
let y = quick_mul(x, n / 2);
return if n % 2 == 0 {
y * y
} else {
y * y * x
};
}
// 这里借鉴了除法的那个,每次都找到能满足的最大的,过了之后就再从1开始找
pub fn my_quick_mul(x: f64, n: i32) -> f64 {
if n == 0 {
return 1.0000;
}
if n == 1 {
return x;
}
let mut count = 1;
let mut res = x;
while count <= n / 2 {
res *= res;
count *= 2;
}
res *= my_quick_mul(x, n - count);
return res;
}终于做出来,虽然复杂度都挺高的,但是也很开心,思路还是深度优先搜索,继续加油。
class Solution {
public List<List<String>> solveNQueens(int n) {
Deque<Integer> path = new ArrayDeque<>();
Deque<boolean[][]> flagStack = new ArrayDeque<>();
List<List<String>> res = new ArrayList<>();
getRes(path, flagStack, res, n);
return res;
}
private void getRes(Deque<Integer> path, Deque<boolean[][]> flagStack, List<List<String>> res, int n) {
if (path.size() == n) {
List<Integer> tempRes = new ArrayList<>(path);
Collections.reverse(tempRes);
List<String> tempStrRes = new ArrayList<>();
for (int i = 0; i < n; i++) {
String str = "";
for (int j = 0; j < n; j++) {
if (tempRes.get(i) == j) {
str += "Q";
} else {
str += ".";
}
}
tempStrRes.add(str);
}
res.add(tempStrRes);
return;
}
boolean[][] oldFlags = new boolean[n][n];
if (!flagStack.isEmpty()) {
oldFlags = flagStack.peek();
}
for (int i = 0; i < n; i++) {
if (oldFlags[path.size()][i]) {
continue;
}
path.push(i);
boolean[][] newFlags = getFlagsFromPath(path, n);
flagStack.push(newFlags);
getRes(path, flagStack, res, n);
path.pop();
flagStack.pop();
}
}
private boolean[][] getFlagsFromPath(Deque<Integer> path, int n) {
boolean[][] flags = new boolean[n][n];
List<Integer> tempRes = new ArrayList<>(path);
Collections.reverse(tempRes);
for (int i = 0; i < tempRes.size(); i++) {
for (int row = 0; row < n; row++) {
for (int col = 0; col < n; col++) {
if (row == i || col == tempRes.get(i) || row - i == col - tempRes.get(i) || row - i == tempRes.get(i) - col) {
flags[row][col] = true;
}
}
}
}
return flags;
}
}写在前面:
x & -x代表除了最后一位1保留,其它位全部变为0;x & (x - 1)代表将最后一位1变为0。
下面做法的本质也是深度优先搜索,不过这个对于棋盘的标记做的很巧妙,其中col、ld、rd分别代表列、左斜下、右斜下,二进制为1代表不能放置,0代表可以放置。
function totalNQueens(n: number): number {
let res: number = 0;
function dfs(n: number, row: number, col: number, ld: number, rd: number) {
if (row >= n) {
res++;
return;
}
// 将所有能放置 Q 的位置由 0 变成 1,以便进行后续的位遍历
let bits = ~(col | ld | rd) & ((1 << n) - 1);
while (bits > 0) {
let pick = bits & -bits;
dfs(n, row + 1, col | pick, (ld | pick) << 1, (rd | pick) >> 1);
bits &= bits - 1;
}
}
dfs(n, 0, 0, 0, 0);
return res;
}我们用$f(i)$表示以坐标i个结尾的子数组的最大和,注意,一定是以坐标i结尾的子数组的最大和,而不是截止到坐标i子数组的最大和,这样我们就不用考虑是否连续的问题了。轻易推出以下方程:
i坐标时,如果$f(i-1)<0$,我们就舍弃掉之前的,只取当前坐标值就行了,这样遍历一次我们就可以求得$f(0)...f(len-1)$,然后我们直接返回最大值就可以。
impl Solution {
pub fn max_sub_array(nums: Vec<i32>) -> i32 {
let mut pre = 0;
let mut res = nums[0];
for v in nums {
pre = max(pre + v, v);
res = max(res, pre);
}
res
}
}加个Python的代码:
class Solution:
def maxSubArray(self, nums: List[int]) -> int:
res = nums[0]
pre = 0
for v in nums:
pre = max(pre + v, v)
res = max(res, pre)
return res自己的解法和官方解法差不多,都是模拟这个过程,就是我这种解法是计算总共会走多少趟,其实可以稍微推导一下,如果是行较少,那么就是二倍的行数-1,如果是列比较少的就是二倍的列数,其他的就没有什么了。
这个和前面那个计算最少多少步能到最后的节点有点像,都是计算在当前节点的可跳范围内,哪个节点能让自己跳的更远。如果一定会跳到0那里就是失败了。现在有点好奇Python是怎么火起来的,写起来真的难受。
class Solution:
def canJump(self, nums: List[int]) -> bool:
index = 0
while index + nums[index] < len(nums) - 1:
if nums[index] == 0:
return False
temp = 0
newIndex = index + 1
for distance in range(1, nums[index] + 1):
if nums[index + distance] + distance < temp:
continue
temp = nums[index + distance] + distance
newIndex = index + distance
index = newIndex
return Truepublic class Solution
{
public bool CanJump(int[] nums)
{
int index = 0;
while (index + nums[index] < nums.Length - 1)
{
if (nums[index] == 0) return false;
int temp = 0;
int newIndex = index + 1;
for (var distance = 1; distance <= nums[index]; distance++)
{
if (nums[index + distance] + distance < temp) continue;
temp = nums[index + distance] + distance;
newIndex = index + distance;
}
index = newIndex;
}
return true;
}
}本题的思路就是先将前两个区间比较,之后将得到的结果再和第三个比较,这样的话就会出现一个比较麻烦的情况,就是如果这个第三个的start和前面两个重叠,这就有点麻烦了,所以我们在最开始将所有的区间按照start增的方式排序就可以了。
public int[][] merge(int[][] intervals) {
if (intervals.length == 0) {
return new int[0][2];
}
Arrays.sort(intervals, new Comparator<int[]>() {
public int compare(int[] interval1, int[] interval2) {
return interval1[0] - interval2[0];
}
});
List<int[]> merged = new ArrayList<>();
for (int[] interval : intervals) {
int L = interval[0], R = interval[1];
if (merged.size() == 0 || merged.get(merged.size() - 1)[1] < L) {
merged.add(new int[]{L, R});
} else {
merged.get(merged.size() - 1)[1] = Math.max(merged.get(merged.size() - 1)[1], R);
}
}
return merged.toArray(new int[merged.size()][]);
}public int[][] Merge(int[][] intervals)
{
var len = intervals.Length;
if (len == 1) return intervals;
Array.Sort(intervals, (interval1, interval2) => interval1[0] - interval2[0]);
var merged = new List<int[]>();
foreach (var interval in intervals)
{
var start = interval[0];
var end = interval[1];
if (merged.Count == 0 || merged[^1][1] < start)
merged.Add(new[] { start, end });
else
merged[^1][1] = Math.Max(merged[^1][1], end);
}
return merged.ToArray();
}C#代码是在太优雅了。
参考上面一题,如果已经是按照左区间排序好的就非常简单的,自己的写法有点复杂,但是问题不大,都是分为三部分,一个是可以直接插入到左边的,然后是需要处理的相交的部分,然后是可以直接插入到右边的。
简单题没有什么好说的,从后往前找就可以了
class Solution:
def lengthOfLastWord(self, s: str) -> int:
index = len(s)-1
while s[index] == ' ':
index -= 1
res = 0
while index >= 0 and s[index] != ' ':
index -= 1
res += 1
return res这题其实也是模拟这个过程,不过吸取了上次官方的经验,直接表示上下左右各在第多少行列,而不是已经占用了多少行列,会好表示一些。
区区困难题,直接深度优先搜索KO!
核心思想就是将首尾连起来,然后再找到新的结尾将next=nil即可。
这题就是一个简单的动态规划,因为只能往右或者往下,所以直接就用左边的节点值+上面的节点值就可以了。
本题和上面一题有点类似,就是需要考虑下什么情况下要跳过当前节点就可以了。
这题和前面的其实还是有点类似,当前位置还是只能从左边和上边过来,如果用核心的还是就这一句:
dp[i][j] = grid[i][j] + Math.min(dp[i - 1][j], dp[i][j - 1]),最后输出dp[m-1][n-1]即可。
说实话这题挺没有意思的,就是模拟这个过程就可以了,希望以后这种题少一些。
没有什么特殊的技巧,模拟这个过程即可。
像十进制一样模拟即可,就是第一位如果也要进的需要注意。
哈哈哈,直接抄的官方的,感觉这题没有意思,虽然是困难题,但是也是模拟这个过程,官方的代码写的很好看,放下:
func blank(n int) string {
return strings.Repeat(" ", n)
}
func fullJustify(words []string, maxWidth int) (ans []string) {
right, n := 0, len(words)
for {
left := right // 当前行的第一个单词在 words 的位置
sumLen := 0 // 统计这一行单词长度之和
// 循环确定当前行可以放多少单词,注意单词之间应至少有一个空格
for right < n && sumLen+len(words[right])+right-left <= maxWidth {
sumLen += len(words[right])
right++
}
// 当前行是最后一行:单词左对齐,且单词之间应只有一个空格,在行末填充剩余空格
if right == n {
s := strings.Join(words[left:], " ")
ans = append(ans, s+blank(maxWidth-len(s)))
return
}
numWords := right - left
numSpaces := maxWidth - sumLen
// 当前行只有一个单词:该单词左对齐,在行末填充剩余空格
if numWords == 1 {
ans = append(ans, words[left]+blank(numSpaces))
continue
}
// 当前行不只一个单词
avgSpaces := numSpaces / (numWords - 1)
extraSpaces := numSpaces % (numWords - 1)
s1 := strings.Join(words[left:left+extraSpaces+1], blank(avgSpaces+1)) // 拼接额外加一个空格的单词
s2 := strings.Join(words[left+extraSpaces+1:right], blank(avgSpaces)) // 拼接其余单词
ans = append(ans, s1+blank(avgSpaces)+s2)
}
}最快的方法肯定是牛顿法,不过自己写的话用二分法就很快了。
impl Solution {
pub fn my_sqrt(x: i32) -> i32 {
if x == 0 || x == 1 {
return x;
}
let x = x as u64;
let mut left = 0;
let mut right = x;
let mut res = 0;
while left <= right {
let mid = (left + right) / 2;
if mid * mid <= x {
res = mid;
left = mid + 1;
} else {
right = mid - 1;
}
}
res as i32
}
}很经典的斐波那契数列问题,不过这种题目如果用递归的话好像会占用更多的栈空间,直接用DP更好点。
public class Solution
{
public int ClimbStairs(int n)
{
if (n is 1 or 2) return n;
var dp = new int[n];
dp[0] = 1;
dp[1] = 2;
for (var i = 2; i < n; i++) dp[i] = dp[i - 1] + dp[i - 2];
return dp[n - 1];
}
}就是区分一些特殊情况,用一个栈就解决了。
首先看到这个题目用DP没有什么问题,就是如何设计状态转移方程比较难。
这里用dp[i][j]表示word1的前i位与word2的前j所需要的编辑距离,那么最开始的边界就是另外一个长度,也就是那两个for循环。
然后就是如何根据目前的值推导出下一个,需要把三种都列出来然后取其中最小的一个,还要注意从dp[i-1][j-1]推导的时候,如果新增的i和j这两个char是相等的,那么就不变,如果变了就+1。
impl Solution {
pub fn min_distance(word1: String, word2: String) -> i32 {
let word1: Vec<char> = word1.chars().collect();
let word2: Vec<char> = word2.chars().collect();
let len1 = word1.len();
let len2 = word2.len();
if len1 == 0 || len2 == 0 {
return max(len1 as i32, len2 as i32);
}
let mut dp = vec![vec![0; len2 + 1]; len1 + 1];
for i in 0..=len1 {
dp[i][0] = i as i32;
}
for i in 0..=len2 {
dp[0][i] = i as i32;
}
for i in 1..=len1 {
for j in 1..=len2 {
let left = dp[i - 1][j] + 1;
let down = dp[i][j - 1] + 1;
let mut left_down = dp[i - 1][j - 1];
if word1[i - 1] != word2[j - 1] {
left_down += 1;
}
dp[i][j] = min(left, min(down, left_down));
}
}
dp[len1][len2]
}
}没啥意思,就是直接先打标签,然后在置零即可。
第一次二分法确定属于第几行,第二次二分法确定即可。
因为这个固定只有1、2、3这三个数字,所以我可以碰到1就往前放,碰到3就往后放,2不用动,同时记录下放的位置,这样一次遍历就解决了。
这题还是比较有意思的,自己也做出来了,和官方的也差不多,都是用滑动窗口。
自己的做法是只维护一个哈希,这个哈希表示字符串中还没有被匹配的情况,但是这种每次都要判断这个有没有匹配成功,应该是这一步比较耗时。
官方的做法是维护两个哈希,同时用一个单独的int类型来记录这个的匹配情况,应该是这一点比我的省时间。
public class Solution
{
public string MinWindow(string s, string t)
{
int sLen = s.Length;
int tLen = t.Length;
if (sLen < tLen) return "";
Dictionary<char, int> tDic = new();
foreach (char c in t)
if (!tDic.ContainsKey(c))
tDic[c] = 1;
else
tDic[c]++;
for (int i = 0; i < tLen; i++)
{
if (!tDic.ContainsKey(s[i])) continue;
tDic[s[i]]--;
}
if (!tDic.Values.Any(v => v > 0)) return s[..tLen];
int tempBegin = 0;
int tempEnd = tLen - 1;
int begin = -1;
int end = sLen;
while (tempBegin < sLen - tLen + 1 && tempEnd < sLen)
{
while (tempEnd - tempEnd > end - begin && tempBegin < sLen - tLen + 1 && tempEnd < sLen)
{
if (tDic.ContainsKey(s[tempBegin]))
{
tDic[s[tempBegin]]++;
}
tempBegin++;
}
if (!tDic.Values.Any(v => v > 0))
{
if (tempEnd - tempBegin + 1 == tLen)
{
return s.Substring(tempBegin, tempEnd - tempBegin + 1);
}
if (tempEnd - tempBegin < end - begin)
{
begin = tempBegin;
end = tempEnd;
}
if (tDic.ContainsKey(s[tempBegin]))
{
tDic[s[tempBegin]]++;
}
tempBegin++;
}
else
{
if (tempEnd < sLen - 1)
{
tempEnd++;
if (tDic.ContainsKey(s[tempEnd]))
{
tDic[s[tempEnd]]--;
}
}
else
{
break;
}
}
}
return begin is -1 ? "" : s.Substring(begin, end - begin + 1);
}
public string MinWindow1(string s, string t)
{
int sLen = s.Length;
int tLen = t.Length;
if (sLen < tLen)
{
return "";
}
Dictionary<char, int> sDic = new();
Dictionary<char, int> tDic = new();
foreach (char c in t)
{
tDic[c] = tDic.ContainsKey(c) ? tDic[c] + 1 : 1;
}
int count = 0;
int start = 0;
int len = int.MaxValue;
for (int tempStart = 0, tempEnd = 0; tempEnd < sLen; tempEnd++)
{
sDic[s[tempEnd]] = sDic.ContainsKey(s[tempEnd]) ? sDic[s[tempEnd]] + 1 : 1;
if (tDic.ContainsKey(s[tempEnd]) && sDic[s[tempEnd]] <= tDic[s[tempEnd]])
{
count++;
}
while (tempStart < tempEnd && (!tDic.ContainsKey(s[tempStart]) || sDic[s[tempStart]] > tDic[s[tempStart]]))
{
sDic[s[tempStart]]--;
tempStart++;
}
// ReSharper disable once InvertIf
if (count == tLen && tempEnd - tempStart + 1 < len)
{
start = tempStart;
len = tempEnd - tempStart + 1;
}
}
return len is int.MaxValue ? "" : s.Substring(start, len);
}
}这题自己的做法还是直接深度优先搜索,但是自己最近几次这种题目的速度都不是很理想,应该是剪枝做的不好,得想办法优化下。
最简单的办法就是分0、1、2...len的情况,然后分别dfs就可以了,懒得去优化了。
这题我的思路是先找到入口,然后通过这个入口进去之后在判断他的四周是否满足下一个字母,如果满足的话就再进入下一层,这个过程中需要注意标记使用情况。
这题我的做法就是判断如果有数连续出现的次数大于2之后就把后面的数复制过来,不过这样其实复杂度挺高的,因为后面其实并不是所有的都需要复制过来的,更简单的做法应该是在复制的时候判断时候有连续出现大于2的数,如果有的话就跳过后续这些大于2的数,接着从这个后面复制,只是说下思路,以后闲的时候想优化的话可以尝试下。
impl Solution {
pub fn remove_duplicates(nums: &mut Vec<i32>) -> i32 {
let len = nums.len();
if len <= 2 {
return len as i32;
}
let mut index = len;
let mut count = 1;
let mut num = nums[0];
let mut i = 1;
while i < index {
if nums[i] == num {
if count < 2 {
count += 1;
i += 1;
} else {
let mut temp_index = i;
// 就是这里,其实并不用一直找到结尾的,而是应该判断后续的数有没有出现大于2的,如果有的话就把后续的数跳过的,这样会少复制些东西,就是判断会比较复杂,但是最终的时间复杂度会小一些。
while temp_index < index && nums[temp_index] == num {
temp_index += 1;
}
for j in 0..len - temp_index {
nums[i + j] = nums[temp_index + j];
}
index = i + index - temp_index;
if i + 1 < index {
num = nums[i];
} else {
return index as i32;
}
count = 1;
i += 1;
}
} else {
num = nums[i];
count = 1;
i += 1;
}
}
index as i32
}
}和前面的那题一样,其实就是划分完之后一部分等于转换的,一部分等于递增的。
但是因为这个里面有重复的元素,所以说需要将重复的情况跳过去:
if (nums[begin] == nums[mid] && nums[mid] == nums[end])
{
begin++;
end--;
}这题的有个难点如果上来就重复的话不是很好处理,这种呢就是需要在前面加一个临时节点,这样最终在返回的时候就返回临时节点的下一个节点即可。
func deleteDuplicates(head *ListNode) *ListNode {
if head == nil || head.Next == nil {
return head
}
pre := &ListNode{
Val: 0,
Next: head,
}
cur := pre
for cur.Next != nil && cur.Next.Next != nil {
if cur.Next.Val == cur.Next.Next.Val {
curNextVal := cur.Next.Val
for cur.Next != nil && cur.Next.Val == curNextVal {
cur.Next = cur.Next.Next
}
} else {
cur = cur.Next
}
}
return pre.Next
}简单题没有什么好说的了。
说实话,没有做出来,CV大法,今天太忙,明天写题解。
这题自己想着用动态规划,用一个二维数组去存当前这个节点的面积已经当前节点的长和宽,但是实际上这种根本就无法得出全部情况,或者说情况太多了(比如竖着或者横着会非常长之类的)。这题和84题都是用的单调栈,最近太忙了都没有时间看,一定要掌握。
这题就是就是设定一个左起点,一个右起点,之后依次往后面塞数就可以了。
需要注意的就是如果全部都在左边或者全部都在右边的特殊情况。
可以用一个四维数组dp[i][j][k][l]表示s1[i..j]和s2[k..l]是否可以相互转换,但是因为必须长度相同才能转换,所以可以简化成dp[i][j][len]表示从s1[i]和s2[j]开始长度为len是否可以相互转换。
class Solution {
public:
bool isScramble(string s1, string s2) {
auto n = s1.length();
auto m = s2.length();
if (n != m) {
return false;
}
vector<vector<vector<bool>>> dp(n, vector<vector<bool>>(n, vector<bool>(n + 1, false)));
// 初始化,就是长度为1的时候
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
dp[i][j][1] = s1[i] == s2[j];
}
}
// 这里的两个为true的条件判断不好理解,第一种就是不对调的,第二种是对调的
for (int len = 2; len <= n; len++) {
for (int i = 0; i <= n - len; i++) {
for (int j = 0; j <= n - len; j++) {
for (int k = 1; k <= len - 1; k++) {
// 不对调的
if (dp[i][j][k] && dp[i + k][j + k][len - k]) {
dp[i][j][len] = true;
break;
}
// 对调的
if (dp[i][j + len - k][k] && dp[i + k][j][len - k]) {
dp[i][j][len] = true;
break;
}
}
}
}
}
return dp[0][0][n];
}
};这题没有说的,直接用了sort,也可以不用,但是嫌麻烦。
这题其实如果把二进制写出来,就可以发现规律了。
后面的其实把前面的先倒过来(不是每个二进制自己倒过来,是原本假设原本四个数是0132,就变成3201),然后再在每个二进制的前面加个1就行。
这题其实还是一个深度优先搜索的问题,就是有两点需要注意:
- 子集和子集之间是不能重复的;
- 子集内可以用重复的数字的。
注意了这两个问题就可以。
class Solution {
public:
vector<vector<int>> subsetsWithDup(vector<int> &nums) {
auto len = nums.size();
vector<vector<int>> res{{}};
if (len == 0) {
return res;
}
// 记得先排序,后面判断重复的时候会用到
sort(nums.begin(), nums.end());
vector<bool> used(len, false);
vector<int> path;
for (int i = 1; i <= len; i++) {
dp(nums, res, used, path, 0, i, len);
}
return res;
}
void dp(vector<int> &nums, vector<vector<int>> &res, vector<bool> &used, vector<int> &path, int begin, int count,
unsigned long long len) {
if (path.size() == count) {
vector<int> temp(path.size());
copy(path.begin(), path.end(), temp.begin());
res.push_back(temp);
return;
}
for (int i = begin; i < len; i++) {
if (used[i] || (count < len && i > 0 && nums[i] == nums[i - 1] && !used[i - 1])) {
continue;
}
path.push_back(nums[i]);
used[i] = true;
dp(nums, res, used, path, i + 1, count, len);
used[i] = false;
path.pop_back();
}
}
};其实和斐波那契数列一样,用一个动态规划就行了,就是需要判断下前面两个字符的匹配情况。
class Solution {
public:
int numDecodings(string s) {
if (s[0] == '0') {
return 0;
}
auto len = s.size();
if (len == 1) {
return s == "0" ? 0 : 1;
}
if (len == 2) {
int temp = stoi(s);
if (temp % 10 == 0 && temp >= 30) {
return 0;
} else if (temp > 26 || temp == 10 || temp == 20) {
return 1;
} else {
return 2;
}
}
vector<int> dp(len + 1, 0);
dp[1] = numDecodings(s.substr(len - 1));
dp[2] = numDecodings(s.substr(len - 2));
for (auto i = 3; i <= len; ++i) {
string tempStr = s.substr(len - i, 2);
int tempNum = numDecodings(tempStr);
// 就是这里需要判断下
if (tempNum == 0) {
dp[i] = 0;
} else if (tempNum == 1) {
if (tempStr == "10" || tempStr == "20") {
dp[i] = dp[i - 2];
} else {
dp[i] = dp[i - 1];
}
} else {
dp[i] = dp[i - 1] + dp[i - 2];
}
}
return dp[len];
}
};和前面的那个反转链表比较像,就是找到起点和终点就可以了。
这个其实也是用深度优先搜索,但是需要一个额外的变量来记录还剩几段。
class Solution {
public:
vector<string> restoreIpAddresses(string s) {
vector<string> res;
auto len = s.length();
if (len < 4 || len > 12) {
return res;
}
vector<string> path;
dfs(s, len, 0, 4, path, res);
return res;
}
void dfs(string s, unsigned long long len, int begin, int residue, vector<string> &path, vector<string> &res) {
if (begin == len) {
if (residue == 0) {
string tempStr;
for (int i = 0; i < path.size() - 1; i++) {
tempStr += path[i] + ".";
}
tempStr += path[path.size() - 1];
res.push_back(tempStr);
return;
}
}
for (int i = begin; i < begin + 3; i++) {
if (i >= len) {
break;
}
if (residue * 3 < len - i) {
continue;
}
if (judgeIpSegment(s, begin, i)) {
string currentIpSegment = s.substr(begin, i - begin + 1);
path.push_back(currentIpSegment);
dfs(s, len, i + 1, residue - 1, path, res);
path.pop_back();
}
}
}
bool judgeIpSegment(string s, int left, int right) {
int len = right - left + 1;
if (len > 1 && s[left] == '0') {
return false;
}
int res = 0;
while (left <= right) {
res = res * 10 + s[left] - '0';
left++;
}
return res >= 0 && res <= 255;
}
};两种方法,一种是递归,一种是手动维护一个栈,其实是一样的,重点是明白中序的意思,就是对于任何一个节点都是先找左边的,再找中间的,然后是右边的,所以用递归最好理解。
class Solution {
public:
// 递归
vector<int> inorderTraversal(TreeNode *root) {
vector<int> res;
inorder(root, res);
return res;
}
void inorder(TreeNode *root, vector<int> &res) {
if (!root) {
return;
}
inorder(root->left, res);
res.push_back(root->val);
inorder(root->right, res);
}
// 手动维护一个栈
vector<int> inorderTraversal1(TreeNode *root) {
vector<int> res;
stack<TreeNode *> stk;
while (root != nullptr || !stk.empty()) {
while (root != nullptr) {
stk.push(root);
root = root->left;
}
root = stk.top();
stk.pop();
res.push_back(root->val);
root = root->right;
}
return res;
}
};二叉树的题目很多可以直接套用递归,这题既然是一个二叉搜索树,那么这个根节点的左右也都是一个二叉搜索树,那么就以这个根节点分别确认左右两边即可。
class Solution {
public:
vector<TreeNode *> generateTrees(int n) {
if (!n) {
return {};
}
return generateTrees(1, n);
}
vector<TreeNode *> generateTrees(int start, int end) {
if (start > end) {
return {nullptr};
}
vector<TreeNode *> allTrees;
// 这里是i就是根节点
for (int i = start; i <= end; i++) {
// 确认左子树
vector<TreeNode *> leftTrees = generateTrees(start, i - 1);
// 确认右子树
vector<TreeNode *> rightTrees = generateTrees(i + 1, end);
// 这里是从左子树中选择一棵
for (auto &left: leftTrees) {
// 这里是从右子树中选择一棵
for (auto &right: rightTrees) {
// 这里就是拼接起来即可
TreeNode *currTree = new TreeNode(i);
currTree->left = left;
currTree->right = right;
allTrees.emplace_back(currTree);
}
}
}
return allTrees;
}
};最笨的方法肯定是将上面的一个求出来再取数,但是这里可以直接用DP
class Solution {
public:
int numTrees(int n) {
std::vector<int> dp(n + 1, 0);
dp[0] = 1;
dp[1] = 1;
for (int i = 2; i <= n; ++i) {
for (int j = 1; j <= i; ++j) {
dp[i] += dp[j - 1] * dp[i - j];
}
}
return dp[n];
}
};一个简单的DP即可,恭贺自己的DP神功小成。
递归即可,就是需要注意下这里传入的值其实是左右节点的值,不是当前节点的值,所以判断也是放在下一次递归里面判断的,不是当次递归。
class Solution {
public:
bool isValidBST(TreeNode* root) {
return helper(root,LONG_MIN,LONG_MAX);
}
bool helper(TreeNode* root,long long lower,long long upper) {
if (root == nullptr){
return true;
}
// 这里其实判断的是上一个节点的左右节点。
if (root->val <= lower ||root->val>= upper){
return false;
}
return helper(root->left,lower,root->val)&&helper(root->right,root->val,upper);
}
};一个二叉搜索树的中序遍历其实就是一个递增数组,所以这题就是先转成数组,再找出来两个元素,然后再在二叉搜索树中找到这两个元素,把值给换了即可。
就是一个简单的递归即可。